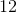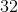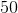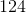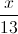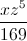$\displaystyle g(f(2))$ is a composite function where $\displaystyle f(2)$ is plugged into $\displaystyle g(x)$:

$\displaystyle f(2)=(2)^{3}-1=8-1=7$

$\displaystyle g(7)=(7)^{2}+1=49+1=50$

First, multiply out the second expression so that you get $\displaystyle 8y^3$.

Then, multiply your like terms, taking care to remember that when multiplying terms that have the same base, you add the exponents. Thus, you get $\displaystyle 24x^9y^{12}$.

Focus on each pair of like terms. The $\displaystyle y's$ completely cancel out, there is one $\displaystyle x$ left on top, and five $\displaystyle z's$ left on the bottom. 

$\displaystyle \frac{13}{169}$ reduces to $\displaystyle \frac{1}{13}$.

Put that all together to get $\displaystyle \frac{xz^5}{13}$. 

Put the negative exponent on the bottom so that you have $\displaystyle \frac{x^{12}}{x^{6}}$ which simplifies further to $\displaystyle x^{6}$.

Use the FOIL method (First, Outer, Inner, Last):

$\displaystyle x * 2x = 2x^2$

$\displaystyle x * 4 = 4x$

$\displaystyle -4 * 2x = -8x$

$\displaystyle -4 * 4 = -16$

Put all of these terms together:

$\displaystyle 2x^2 + 4x - 8x - 16$

Combine like terms:

$\displaystyle 2x^2 - 4x - 16$

To simplify the polynomial, begin by multiplying the first binomial by every term within the parentheses:

$\displaystyle ab^{-2}(a^2b+a^{-1}b^3-a^3b^{-1})$

$\displaystyle aa^2b^{-2}b+aa^{-1}b^{-2}b^3-aa^3b^{-2}b^{-1}$

Now, combine like terms:

$\displaystyle a^3b^{-1}+b^1-a^4b^{-3}$

Convert the polynomial into fraction form:

$\displaystyle \frac{a^3}{b}+b-\frac{a^4}{b^3}$

To simplify the polynomial, begin by rearranging the terms to have positive exponents:

$\displaystyle \frac{-18a^{-2}b^3c^{-4}}{12ab^{-2}c^{-3}}$

$\displaystyle \frac{-18b^3b^2c^{3}}{12aa^2c^{4}}$

Now, combine like terms:

$\displaystyle \frac{-18b^5}{12a^3c^{1}}$

Simplify the integers:

$\displaystyle \frac{-3b^5}{2a^3c}$

Squaring the polynomial is equivalent to:

$\displaystyle (5n^{3x}-2m^{x+2})^2$

$\displaystyle (5n^{3x}-2m^{x+2})(5n^{3x}-2m^{x+2})$

Use the FOIL method to multiply the terms:

F - First

O - Outer

I - Inner

L - Last

$\displaystyle 25n^{6x}-10n^{3x}m^{x+2}-10n^{3x}m^{x+2}+4m^{2x+4}$

Combine like terms:

$\displaystyle 25n^{6x}-20n^{3x}m^{x+2}+4m^{2x+4}$

To simplify the polynomial, begin by rearranging the terms to have positive exponents:

$\displaystyle (\frac{-a^{-2}b^3c^{-1}}{3a^{-4}b^{-1}c^3})^{-2}$

$\displaystyle (\frac{-a^{4}b^3b^1}{3a^{2}c^3c^1})^{-2}$

Rearrange the terms once again so that the outer exponent is positive. Also, combine like terms:

$\displaystyle (\frac{-3c^4}{a^{2}b^4})^{2}$

Now, square the polynomial:

$\displaystyle \frac{9c^8}{a^{4}b^8}$

To simplify the polynomial, begin by combining the terms within the parentheses and multiplying the integers:

$\displaystyle (5a)(6a^2b)(3ab^3)+(2a)^2(3b^3)(2a^2b)$

$\displaystyle 90a^4b^4+24a^4b^4$

Now, add together like terms:

$\displaystyle 90a^4b^4+24a^4b^4=114a^4b^4$