All High School Math Resources
Example Questions
Example Question #1 : Derivatives
The speed of a car traveling on the highway is given by the following function of time:
Note that
What does this mean?
The car is not accelerating at time 
The car is not decelerating at time 
The car is not moving at time 
The car's speed is constantly changing at time 
The car takes 
The car is not moving at time 
The function 






Example Question #1 : Conceptualizing Derivatives
The speed of a car traveling on the highway is given by the following function of time:
Consider a second function:
What can we conclude about this second function?
It represents the rate at which the speed of the car is changing.
It has no relation to the previous function.
It represents another way to write the car's speed.
It represents the change in distance over a given time 
It represents the total distance the car has traveled at time 
It represents the rate at which the speed of the car is changing.
Notice that the function 

Therefore, 
Example Question #41 : Second Derivatives
Define 
Give the interval(s) on which 

<0)
We need to find the values of 
&space;=&space;3x%5E%7B2%7D&space;-18x+24&space;<0)
These are the boundary points, so the intervals we need to check are:


We check each interval by substituting an arbitrary value from each for 
Choose

Choose

Choose

The answer is that 

Example Question #2 : Finding Regions Of Increasing And Decreasing Value
Define &space;=&space;x%5E%7B3%7D&space;-&space;%5Cfrac%7B21%7D%7B2%7D&space;x%5E%7B2%7D&space;+30x&space;-6)
Give the interval(s) on which 

>0)
We need to find the values of 

These are the boundary points, so the intervals we need to check are:


We check each interval by substituting an arbitrary value from each for 
Choose

Choose

Choose

The answer is that 
Example Question #1 : Finding Regions Of Increasing And Decreasing Value
At what point does 
It does not shift from increasing to decreasing
To find out where the graph shifts from increasing to decreasing, we need to look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
We're going to treat 

Notice that 
If we were to graph 
Example Question #1 : Derivatives
At what point does 
To find out where it shifts from decreasing to increasing, we need to look at the first derivative. The shift will happen where the first derivative goes from a negative value to a positive value.
To find the first derivative for this problem, we can use the power rule. The power rule states that we lower the exponent of each of the variables by one and multiply by that original exponent.
Remember that anything to the zero power is one.
Can this equation be negative? Yes. Does it shift from negative to positive? Yes. Therefore, it will shift from negative to positive at the point that 
Example Question #42 : Second Derivatives
At what value of 

It does not shift from decreasing to increasing
To find out when the function shifts from decreasing to increasing, we look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
Anything to the zero power is one.
From here, we want to know if there is a point at which graph changes from negative to positive. Plug in zero for y and solve for x.
This is the point where the graph shifts from decreasing to increasing.
Example Question #1 : Finding Regions Of Concavity And Convexity
At the point 

The function is undefined at that point
Increasing, concave
Decreasing, convex
Increasing, convex
Decreasing, concave
Decreasing, convex
First, let's find out if the graph is increasing or decreasing. For that, we need the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
We're going to treat 

Notice that 
Plug in our given point for 
Our result is negative, therefore the function is decreasing.
To find the concavity, look at the second derivative. If the function is positive at our given point, it is concave. If the function is negative, it is convex.
To find the second derivative we repeat the process, but using 
As you can see, our second derivative is a constant. It doesn't matter what point we plug in for 
Combine our two pieces of information to see that at the given point, the graph is decreasing and convex.
Example Question #1 : Finding Regions Of Concavity And Convexity
Let 
This question asks us to examine the concavity of the function 
Let us begin by finding the first derivative of f(x). We will need to use the Product Rule. According to the Product Rule, if 



In order to evaluate the derivative of 





We can now finish finding the derivative of the original function.
To summarize, the first derivative of the funciton 

We need the second derivative in order to examine the concavity of f(x), so we will differentiate one more time. Once again, we will have to use the Product Rule in conjunction with the Chain Rule.
In order to find where f(x) is concave upward, we must find where f''(x) > 0.
In order to solve this inequality, we can divide both sides by 


Dividing both sides of the inequality by 
When solving inequalities with polynomials, we often need to factor.
Notice now that the expression 



Thus, the second derivative of f''(x) will be positive (and f(x) will be concave up) only when 

The answer is 
Example Question #2 : Finding Regions Of Concavity And Convexity
At the point 

Decreasing, convex
Increasing, concave
Decreasing, concave
The graph is undefined at point
Increasing, convex
Decreasing, convex
To find out if the function is increasing or decreasing, we need to look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
Anything to the zero power is one.
Now we plug in our given value and find out if the result is positive or negative. If it is positive, the function is increasing. If it is negative, the function is decreasing.
Therefore, the function is decreasing.
To find out if it is concave or convex, look at the second derivative. If the result is positive, it is convex. If it is negative, then it is concave.
To find the second derivative, we repeat the process using 
We're going to treat 

Notice that 
As stated before, anything to the zero power is one.
Since we get a positive constant, it doesn't matter where we look on the graph, as our second derivative will always be positive. That means that this graph is going to be convex at our given point.
Therefore, the function is decreasing and convex at our given point.
Certified Tutor
All High School Math Resources








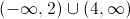

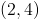

&space;=&space;3%5Ccdot&space;x%5E%7B3-1%7D&space;-2%5Ccdot&space;9x%5E%7B2-1%7D+24+0)


























































































![f'(x)=\left (\frac{\mathrm{d} }{\mathrm{d} x}[x] \right )\cdot e^{x^2}+\left (\frac{\mathrm{d} }{\mathrm{d} x}[e^{ x^2}] \right )\cdot x](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/103021/gif.latex)
![f'(x)=1\cdot e^{x^2}+\left (\frac{\mathrm{d} }{\mathrm{d} x}[e^{ x^2}] \right )\cdot x](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/110466/gif.latex)
![\frac{\mathrm{d} }{\mathrm{d} x}[e^{x^2}]=e^{x^2}\cdot \frac{\mathrm{d} }{\mathrm{d} x}[x^2]=2x\cdot e^{x^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/103025/gif.latex)
![f'(x)=1\cdot e^{x^2}+\left (\frac{\mathrm{d} }{\mathrm{d} x}[e^{ x^2}] \right )\cdot x](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/116585/gif.latex)

![f''(x)=\frac{\mathrm{d} }{\mathrm{d} x}[f'(x)]=\left (\frac{\mathrm{d} }{\mathrm{d} x}[e^{x^2}] \right )\cdot(2x^2+1)+\left (\frac{\mathrm{d} }{\mathrm{d} x} [ 2x^2+1] \right ) \cdot e^{x^2 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/116586/gif.latex)






















