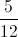All High School Math Resources
Example Questions
Example Question #12 : Midpoint And Distance Formulas
What is the length of a line with endpoints 

Possible Answers:
Correct answer:
Explanation:
The formula for the length of a line is very similiar to the pythagorean theorem:
Plug in our given numbers to solve:
Example Question #11 : Lines
The points A, B, and C reside on a line segment. B is the midpoint of AC. If line AB measures 6 units in length, what is the length of line AC?
Possible Answers:
Correct answer:
Explanation:
If B is the midpoint of AC, then AC is twice as long as AB. We are told that AB=6.
The diagram shows six units between points A and B, with B as the midpoint of segment AC. Therefore segment BC is also six units long, so line AC is twelve units long.
All High School Math Resources
Popular Subjects
ACT Tutors in Chicago, Calculus Tutors in Miami, LSAT Tutors in Miami, Physics Tutors in Seattle, French Tutors in Chicago, Spanish Tutors in Philadelphia, Calculus Tutors in New York City, Calculus Tutors in San Diego, Computer Science Tutors in Los Angeles, Chemistry Tutors in Philadelphia
Popular Courses & Classes
GRE Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Atlanta, ISEE Courses & Classes in Atlanta, ISEE Courses & Classes in Phoenix, MCAT Courses & Classes in Miami, GRE Courses & Classes in New York City, SAT Courses & Classes in New York City, ACT Courses & Classes in Miami, Spanish Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in San Diego
Popular Test Prep
LSAT Test Prep in Miami, ISEE Test Prep in San Francisco-Bay Area, LSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Houston, SAT Test Prep in Phoenix, LSAT Test Prep in Atlanta, SAT Test Prep in Philadelphia, MCAT Test Prep in Denver, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Houston