All High School Math Resources
Example Questions
Example Question #1 : Exponents
Which of the following is equivalent to 
By definition,

In our problem, 

Then, we have 
Example Question #93 : Algebra Ii
Solve for 
Raise both sides of the equation to the inverse power of 
Subtract 
Example Question #1 : Exponents
Convert the exponent to radical notation.
Remember that exponents in the denominator refer to the root of the term, while exponents in the numerator can be treated normally.
Example Question #94 : Algebra Ii
Which of the following is equivalent to 
By definition, a number raised to the 
Since the square root of 64 is 8, 8 is our solution.
Example Question #1 : Fractional Exponents
Simplify the expression:
Remember that fraction exponents are the same as radicals.
A shortcut would be to express the terms as exponents and look for opportunities to cancel.
Either method, we then need to multiply to two terms.
Example Question #1 : Simplifying Exponents
Simplify the following expression.
When dividing with exponents, the exponent in the denominator is subtracted from the exponent in the numerator. For example: 
In our problem, each term can be treated in this manner. Remember that a negative exponent can be moved to the denominator.
Now, simplifly the numerals.
Example Question #1 : Simplifying Exponents
Simplify the following expression.
We are given: 
Recall that when we are multiplying exponents with the same base, we keep the base the same and add the exponents.
Thus, we have 
Example Question #1 : Simplifying Exponents
Simplify the following expression.
Recall that when we are dividing exponents with the same base, we keep the base the same and subtract the exponents.
Thus, we have 
We also recall that for negative exponents,

Thus, 
Example Question #9 : Exponents
Simplify the following exponent expression:
Begin by rearranging the terms in the numerator and denominator so that the exponents are positive:
Multiply the exponents:
Simplify:
Example Question #2 : Exponents
Simplify the expression:
First simplify the second term, and then combine the two:
Certified Tutor
Certified Tutor
All High School Math Resources



















![\small \small \sqrt[7]{x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/39746/gif.latex)
![\small \small \sqrt[3]{x^7}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/39747/gif.latex)
![x^{\frac{a}{b}}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88792/gif.latex)
![x^{\frac{3}{7}}=\sqrt[7]{x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/110623/gif.latex)






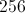




![256^{\frac{3}{4}}=\sqrt[4]{256^3}=64](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/113588/gif.latex)