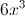Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Solving Equations

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Equations

Cindy's Cotton Candy sells cotton candy by the bag. Her monthly fixed costs are $\$150$ . It costs $\$2.50$ to make each bag and she sells them for $\$4.00$ .

What is the monthly break-even point?

Possible Answers:

$225\; bags$

$60\; bags$

$100\; bags$

$150\; bags$

$80\; bags$

Correct answer:

$100\; bags$

Explanation:

Costs=150+2.50x

Revenues = 4.00x

The break-even point occurs when the costs=revenues .

The equation to solve becomes

4x=150+2.5x so the break-even point is $100 \; bags$ .

Report an Error

Example Question #1 : Equations

Cindy's Cotton Candy sells cotton candy by the bag. Her monthly fixed costs are $\$150$ . It costs $\$2.50$ to make each bag and she sells them for $\$4.00$ .

To make a profit of $\$150$ , how many bags of cotton candy must be sold?

Possible Answers:

$250\; bags$

$200\; bags$

$100\; bags$

$300\; bags$

$150\; bags$

Correct answer:

$200\; bags$

Explanation:

Costs=150+2.50x

Revenues = 4.00x

Profits = Revenues - Costs = 4x - (150+2.5x)=1.5x -150

So the equation to solve becomes 150 = 1.5x - 150 , or $x=200\; bags$ must be sold to make a profit of $\$150$ .

Report an Error

Example Question #3 : Equations

Solve for and to satisfy both equations in the system:

$\begin{Bmatrix} 6x+y = 25 \\ 2x-3y = 25 \end{Bmatrix}$

Possible Answers:

x=5 , y = 5

x = 5 , y= -5

x = -5 , y = 5

x= -5 , y = -5

x = 3 , y = 7

Correct answer:

x = 5 , y= -5

Explanation:

The two equations in this system can be combined by addition or subtraction to solve for and . Isolate the variable to solve for it by multiplying the top equation by so that when the equations are combined the term disappears.

$3\times(6x + y = 25)$

$\rightarrow 18x+3y = 75$

$\rightarrow (18x +3y = 75) + (2x - 3y = 25)$

$\rightarrow 20x = 100$

Divide both sides by to find as the value for .

Substituting for in both of the two equations in the system and solving for gives a value of for .

Report an Error

Example Question #1 : Solving Equations

Solve for :

$\left | 12x - 39 \right | = 60$

Possible Answers:

$x = - 8 \frac{1}{4} \textrm{ or }x = 8 \frac{1}{4}$

$x = -1 \frac{3}{4} \textrm{ or }x = 8 \frac{1}{4}$

$x = 1 \frac{3}{4} \textrm{ or }x = 8 \frac{1}{4}$

$x = 8 \frac{1}{4}$

$x = 1 \frac{3}{4}$

Correct answer:

$x = -1 \frac{3}{4} \textrm{ or }x = 8 \frac{1}{4}$

Explanation:

Rewrite $\left | 12x - 39 \right | = 60$ as a compound statement and solve each part separately:

$\left | 12x - 39 \right | = 60$

$12x - 39 = - 60 \textrm{ or }12x - 39 = 60$

12x - 39 = - 60

12x - 39 + 39 = - 60+ 39

12x = - 21

$12x \div 12 = - 21 \div 12$

$x = -1 \frac{3}{4}$

12x - 39 = 60

12x - 39 + 39 = 60+ 39

12x = 99

$12x \div 12 = 99 \div 12$

$x = 8 \frac{1}{4}$

The solution set is $\left \{ -1 \frac{3}{4} ,8 \frac{1}{4}\right \}$

Report an Error

Example Question #1 : Equations

a^2-b^2 = 33 and a-b=3 . What is the value of $a^{2}+b^{2}$ ?

Possible Answers:

130

112

Correct answer:

Explanation:

First, notice that we can factor a^2-b^2 into the form (a-b)(a+b). We are told that a-b=3, so we can substitute that into the first equation.

(a-b)(a+b)=33

3(a+b)=33

If we divide both sides by 3, we can obtain the value of a+b.

a+b=11

We now have a system of equations: a-b = 3, a+b = 11. We will solve this system by elimination. If we add the two equations together, we obtain the following:

2a=14 .

Divide both sides by 2.

a=7.

Going back to the equation a-b = 7, we can solve for b.

7-b=3

Add b to both sides.

7=3+b

Subtract 3 from both sides.

b=4.

Ultimately, the question asks us to determine the value of a^2+b^2 .

a^2+b^2 = $7^{2}+4^{2}=49+16=65$ .

The answer is 65.

Report an Error

Example Question #2 : Solving Equations

Solve the pair of equations for x and y:

x+y=4

x-y=8

Possible Answers:

x=-6,y=2

x=-6,y=-2

x=6, y=-2

x=-2,y=6

x=2,y=-6

Correct answer:

x=6, y=-2

Explanation:

Equation 1: x+y=4

Equation 2: x-y=8

Solve equation 2 for X: x=8+y

Substitute into Equation 1: (8+y)+y=4

Solve for y: 2y=-4 , y=-2

Take the answer for y and plug it back into either original equation to find x:

x=6, y=-2

Report an Error

Example Question #3 : Solving Equations

Solve the pair of equations for x and y:

2x+y=16

y-2x=0

Possible Answers:

x=8,y=-4

x=8,y=4

x=4,y=-8

x=-4,y=8

x=4,y=8

Correct answer:

x=4,y=8

Explanation:

Equation 1: 2x+y=16

Equation 2: y-2x=0

Solve Equation 2 for y:

y=2x

Substitute into Equation 1:

2x+2x=16

4x=16

x=4

Plug x back into either original equations and solve for y:

x=4,y=8

Report an Error

Example Question #3 : Solving Equations

For which of the following functions is the result of f(-2) a positive integer?

Possible Answers:

2x-10

6x^3

2x^2-13

2x-5

5x^2 + 2

Correct answer:

5x^2 + 2

Explanation:

Simply plugging in -2 into each answer choice will determine the correct answer:

6x^3 = 6(-2)^3 = -48

2x-5=2(-2)-5=-9

2x^2-13=2(-2)^2-13=-5

5x^2 + 2 = 5(-2)^2 + 5 = 25

2x-10 = 2(-2) - 10 = -14

The key to solving this problem is to remember the order of operations and that negative numbers squared are positive, while negative numbers raised to the third power are negative.

Report an Error

Example Question #4 : Solving Equations

Given the equation x^3 -6 = 210 , what is the value of 2x + 3 ?

Possible Answers:

Correct answer:

Explanation:

When solving the equation x^3 - 6 = 210 , observe that x^3 = 216 . Taking the cube root of 216 gives 6. Thus, 2x + 3=2(6) + 3=15.

Report an Error

Example Question #5 : Solving Equations

A cardboard packing box contains footballs and baseballs. The ratio by weight of baseballs to footballs is 7 to 9. How many kilograms of footballs will there be in the box if the total weight of the box is 48 kilograms?

Possible Answers:

Correct answer:

Explanation:

In the box, there are kilograms of baseballs and kilograms of footballs. In total, there are 16x kilograms of balls. The total weight of the box is 48 kilograms, so $16x = 48\: and\: x = 3.$ Since there are kilograms of footballs, the total weight of the footballs in the box is equal to: 9(3) = 27.

Report an Error

View Tutors

Ronald
Certified Tutor

Towson University, Master of Science, Counseling Psychology.

View Tutors

Jonathan
Certified Tutor

East Carolina University, Bachelor of Science, Chemistry. East Carolina University, Bachelor of Science, Biology, General.

View Tutors

Constance
Certified Tutor

Loyola University-Chicago, Bachelors, Psychology. Sam Houston State University, Masters, Counseling Psychology.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in San Francisco-Bay Area, GMAT Tutors in Miami, Computer Science Tutors in Chicago, Calculus Tutors in Houston, Physics Tutors in San Diego, Biology Tutors in Dallas Fort Worth, SAT Tutors in San Diego, English Tutors in Phoenix, English Tutors in Chicago, Algebra Tutors in Phoenix

Popular Courses & Classes

GMAT Courses & Classes in Los Angeles, LSAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Boston, LSAT Courses & Classes in Denver, GMAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in New York City, MCAT Courses & Classes in Boston, ISEE Courses & Classes in Denver, GRE Courses & Classes in New York City, SSAT Courses & Classes in Chicago

Popular Test Prep

SSAT Test Prep in Boston, GMAT Test Prep in New York City, LSAT Test Prep in Denver, GRE Test Prep in New York City, ISEE Test Prep in Seattle, SAT Test Prep in San Diego, GMAT Test Prep in Denver, SAT Test Prep in Miami, GRE Test Prep in San Diego, SSAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Solving Equations

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Equations

Example Question #1 : Equations

Example Question #3 : Equations

Example Question #1 : Solving Equations

Example Question #1 : Equations

Example Question #2 : Solving Equations

Example Question #3 : Solving Equations

Example Question #3 : Solving Equations

Example Question #4 : Solving Equations

Example Question #5 : Solving Equations

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: