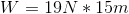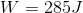All High School Physics Resources
Example Questions
Example Question #1 : Calculating Work
A 

The formula for work is 
In this case, there is only one force acting upon the object: the force due to gravity. Plug in our given information for the distance to solve for the work done by gravity.
Remember, since the object will be moving downward, the distance should be negative.
The work done is positive because the distance and the force act in the same direction.
Example Question #3 : Work
A 

Work is a force times a distance:
We know the distance that the book needs to travel, but we need to sovle for the lifting force required to move it.
There are two forces acting upon the book: the lifting force and gravity. Since the book is moving with a constant velocity, that means the net force will be zero. Mathemetically, that would look like this:
We can expand the right side of the equation using Newton's second law:
Use the given mass and value of gravity to solve for the lifting force.
Now that we have the force and the distance, we can solve for the work to lift the book.
This problem can also be solved using energy. Work is equal to the change in potential energy:
While on the ground, the book has zero potential energy. Once back on the shelf, the energy is equal to 

Example Question #1 : Work
A 

Work is a force times a distance:
We know the distance that the book needs to travel, but we need to sovle for the lifting force required to move it.
There are two forces acting upon the book: the lifting force and gravity. Since the book is moving with a constant velocity, that means the net force will be zero. Mathemetically, that would look like this:
We can expand the right side of the equation using Newton's second law:
Use the given mass and value of gravity to solve for the lifting force.
Now that we have the force and the distance, we can solve for the work to lift the book.
This problem can also be solved using energy. Work is equal to the change in potential energy:
While on the ground, the book has zero potential energy. Once back on the shelf, the energy is equal to 

Example Question #2 : Calculating Work
A 

Work is a force times a distance:
We know the distance that the book needs to travel, but we need to sovle for the lifting force required to move it.
There are two forces acting upon the book: the lifting force and gravity. Since the book is moving with a constant velocity, that means the net force will be zero. Mathemetically, that would look like this:
We can expand the right side of the equation using Newton's second law:
Use the given mass and value of gravity to solve for the lifting force.
Now that we have the force and the distance, we can solve for the work to lift the book.
This problem can also be solved using energy. Work is equal to the change in potential energy:
While on the ground, the book has zero potential energy. Once back on the shelf, the energy is equal to 

Example Question #1 : Calculating Work
A cat knocks a 


The relationship between work, force, and distance is:
We are given the force on the toy and the work done. Using these values, we can find the distance. Note that the mass is not relevant for this question.
Example Question #71 : Energy And Work
A cat knocks a 


The relationship between work, force and distance is:
We are given the value for the force and the distance that the toy travels. Using these values, we can find the work done by the cat. Note that the mass of the toy is not relevant for this calculation.
Example Question #2 : Calculating Work
A cat knocks a 


The relationship between work, force and distance is:
We are given the value for the work done by the cat and the distance that the toy travels. Using these values, we can find the force on the toy. Note that the mass of the toy is not relevant for this calculation.
Example Question #72 : Energy And Work
A 


The formula for work is:
Given the values for force and distance, we can calculate the work done.
Note that no work is done by the force of gravity or the weight of the box, since the vertical position does not change.
Example Question #3 : Calculating Work
Ryan pushes a 


Work is the product of force times a distance:
We are given the work and the distance traveled, allowing us to solve for the force. The mass of the cabinet is not necessary information.
Example Question #473 : High School Physics
A 1500kg rocket has a net propulsion force of 500N. Over a short period of time, the rocket speeds up uniformly from an initial velocity of 

None of these
Use the data given to calculate the kinetic energy of the rocket at the two different velocities. Then find the amount of work done using the following equation:
Kinetic energy of the rocket at the two velocities:
The change in the kinetic energy at the two velocities:

Certified Tutor
Certified Tutor
All High School Physics Resources