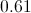When multiplying decimals you ignore the decimals and multiply the two numbers like you would normally.

Then count the total number of decimal places to the right of the decimal of the original numbers.

Move the decimal from the whole number answer you just received to the left the same number of times as the total decimal places to the right of the numbers before you multiplied them.

Therefore the answer is $\displaystyle .18$ 

Examine the divisor 0.004. To make this a whole number, the decimal point needs to be moved three places right. Do this to both 0.004 and 320, adding an implied decimal point after the latter first:

$\displaystyle 320.000 \div 0.004 \Rightarrow 320000. \div 4$

Now perform this division:

$\displaystyle 320,000. \div 4 = 80,000$

$\displaystyle 0.3^{5} = 0.3 \cdot 0.3\cdot 0.3\cdot 0.3\cdot 0.3$

First, multiply, ignoring the decimal points:

$\displaystyle 3 \cdot 3\cdot 3\cdot 3\cdot 3 = 243$

Put a decimal point after the number:

$\displaystyle 243.$

Since there were five digits total (one per factor) left of the decimal points, move the decimal point in the product left five places, inserting zeroes as needed:

$\displaystyle 0.00243$

The fraction has its last nonzero digit in the hundredths place, so write the number, without the decimal point, over 100. Then reduce.

$\displaystyle \frac{114}{100} = \frac{114\div 2}{100\div 2} = \frac{57}{50}$

To rewrite a very large number in scientific notation:

Write the number with the decimal point after it (it is implied to be at that location).

$\displaystyle 450,000,000,000.$

Move the decimal point left as many places as needed until it follows the first nonzero digit, which here is the four. Count the number of places it is moved - here it will be eleven places.

The number formed is $\displaystyle 4.5$, which will be placed in front; 11, the number of places counted, will be the exponent. The number, in scientific notation, will be $\displaystyle 4.5 \times 10^{11}$.

Multiply normally and remember that the decimal point is four places from the right. 

Divide 8 by 15:

 $\displaystyle \frac{8}{15} = 8 \div 15 = 0.5333...$ 

The 3 repeats, so the correct choice is $\displaystyle 0.5\overline{3}$.

Divide 11 by 18:

$\displaystyle \frac{11}{18} = 11 \div 18 = 0.61111...$

The 1 repeats infinitely, so this can be rewritten as $\displaystyle 0.6\overline{1}$.

Divide 5 by 27:

$\displaystyle \frac{5}{27} = 5 \div 27 = 0.185185185...$

The group "185" repeats infinitely, so this can be written as $\displaystyle 0.\overline{185}$.

Divide 7 by 36: 

$\displaystyle \frac{7}{36} = 7 \div 36 = 0.19444444...$

The 4 repeats infinitely, so this can be rewritten as $\displaystyle 0.19\overline{4}$.