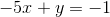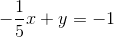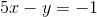Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : How to find the equation of a curve

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Equation Of A Curve

If a line's -intercept is . and the -intercept is , what is the equation of the line?

Possible Answers:

-5x+y=-1

$-\frac{1}{5}x+y=\frac{1}{5}$

5x-y=-1

$-\frac{1}{5}x+y=-1$

$\frac{1}{5}x-\frac{1}{5}y=-1$

Correct answer:

$-\frac{1}{5}x+y=-1$

Explanation:

Write the equation in slope-intercept form:

y=mx+b

We were given the -intercept, , which means b=-1 :

y=mx-1

Given the -intercept is , the point existing on the line is (5,0) . Substitute this point into the slope-intercept equation and then solve for to find the slope:

0=m(5)-1

Add to each side of the equation:

1=5m

Divide each side of the equation by :

$m=\frac{1}{5}$

Substituting the value of back into the slope-intercept equation, we get:

$y=\frac{1}{5}x-1$

By subtracting $-\frac{1}{5}x$ on both sides, we can rearrange the equation to put it into standard form:

$-\frac{1}{5}x+y=-1$

Report an Error

Example Question #1 : How To Find The Equation Of A Curve

Find the -intercept of:

y=4x+2

Possible Answers:

x=-2

x=1

x=0.5

x=-0.5

x=2

Correct answer:

x=-0.5

Explanation:

To find the x-intercept, we need to find the value of when y=0 .

So we first set to zero.

y=4x+2

turns into

0=4x+2

Lets subtract from both sides to move to one side of the equation.

-4x=4x-4x+2

After doing the arithmetic, we have

-4x=2 .

Divide by from both sides

$\frac{-4x}{-4}=\frac{2}{-4}$

x=-0.5

Report an Error

Example Question #1 : How To Find The Equation Of A Curve

What is the -intercept of:

y=x^2+x+9

Possible Answers:

y=10

x=9

x=2

y=9

y=-9

Correct answer:

y=9

Explanation:

To find the y-intercept, we set x=0

y=x^2+x+9

turns into

y=0^2+0+9 .

After doing the arithmetic we get

y=9 .

Report an Error

Example Question #2 : How To Find The Equation Of A Curve

What is the -intercept of:

y=3x+3

Possible Answers:

y=1

x=1

x=-1

y=-1

x=0

Correct answer:

x=-1

Explanation:

The x-intercept can be found where y=0

y=3x+3

turns into

0=3x+3 .

Lets subtract from both sides to solve for .

-3x=3x-3x+3

After doing the arithmetic we have

-3x=3 .

Divide both sides by

$\frac{-3x}{-3}=\frac{3}{-3}$

x=-1

Report an Error

Example Question #3 : How To Find The Equation Of A Curve

Suppose two intercepts create a line. If the -intercept is and -intercept is , what is the equation of the line?

Possible Answers:

y=2x+2

$y=-\frac{1}{2}x+2$

y=-2x+2

x-2y=0

$y=\frac{1}{2}x+2$

Correct answer:

y=-2x+2

Explanation:

Rewrite the intercepts in terms of points.

X-intercept of 1: (1,0) .

Y-intercept of 2: (0,2)

Write the slope-intercept form for linear equations.

y=mx+b

Substititute the y-intercept into the slope-intercept equation.

2=m(0)+b

b=2

Substitute both the x-intercept point and the y-intercept into the equation to solve for slope.

0=m(1)+2

-2=m

Rewrite by substituting the values of and into the y-intercept form.

y=-2x+2

Report an Error

Example Question #1 : How To Find The Equation Of A Curve

Which equation has a y-intercept at 2 and x-intercepts at -1 and 6?

Possible Answers:

$\small y = -3(x+1)(x-2)$

$\small y = \frac{-1}{3}(x+1)(x-6)$

$\small y = \frac{1}{3}(x-1)(x+6)$

$\small y=3 (x+1)(x-2 )$

$\small \small y = (x+1)(x-6)$

Correct answer:

$\small y = \frac{-1}{3}(x+1)(x-6)$

Explanation:

In order for the equation to have x-intercepts at -1 and 6, it must have $\small (x+1)$ and (x-6) as factors. This leaves us with only 2 choices, $\small \small y = (x+1)(x-6)$ or $\small y = \frac{-1}{3}(x+1)(x-6)$

This equation must also have a y-intercept of 2. This means that plugging in 0 for x will gives us a y-value of 2. Because we have two options, we could plug in 0 for x in each to see which gives us an answer of 2:

a) $\small y = (0+1)(0-6) = 1*-6 = -6$ we can eliminate that choice

b) $\small y= -\frac{1}{3}(0+1)(0-6) = -\frac{1}{3}*1*-6 = 2$ this must be the right choice.

If we hadn't been given multiple options, we could have set up the following equation to figure out the third factor:

$\small 2 = C(0+1)(0-6)$

$\small 2 = C*1*-6$

$\small 2 = -6C$ divide by -6

$\small -\frac{1}{3} = C$

Report an Error

Example Question #2 : How To Find The Equation Of A Curve

Which equation would have an x-intercept at $\small x=2$ and a y-intercept at $\small y=-3$ ?

Possible Answers:

$y = \frac{2}{3}x - 3$

$\small y = \frac{3}{2}x - 3$

$\small y = \frac{3}{2}x + 3$

$\small y = -\frac{3}{2}x - 3$

$\small y = -\frac{2}{3}x + 2$

Correct answer:

$\small y = \frac{3}{2}x - 3$

Explanation:

We're writing the equation for a line passing through the points $\small (0,-3)$ and $\small (2,0)$ . Since we already know the y-intercept, we can figure out the slope of this line and then write a slope-intercept equation.

To determine the slope, divide the change in y by the change in x:

$\small \frac{-3 - 0 }{ 0 - 2 } = \frac{-3}{-2} = \frac{3}2$

The equation for this line would be $\small y = \frac{3}{2}x - 3$ .

Report an Error

Example Question #2 : How To Find The Equation Of A Curve

Write the equation of a line with intercepts (0, 4) and (-1, 0 )

Possible Answers:

y = 4x + 4

$y = -\frac{1}{4}x + 1$

y = 5x-1

y = -x+5

$y = \frac{1}{4}x +1$

Correct answer:

y = 4x + 4

Explanation:

The line will eventually be in the form y = mx+b where is the y-intercept.

The y-intercept in this case is .

To find the equation, plug in for , and the other point, (-1,0) as x and y:

0 = m(-1)+ 4

0 = -m + 4 add to both sides

m = 4

This means the equation is y = 4x + 4

Report an Error

Example Question #2 : How To Find The Equation Of A Curve

Which equation has the x- and y-intercepts (2,0) and (0,7) ?

Possible Answers:

$y = \frac{2}{7} x + 2$

$y = \frac{7}{2} x +3$

$y = -\frac{2}{7} + 3$

$y = -\frac{7}{2}x + 7$

y = 5x + 1

Correct answer:

$y = -\frac{7}{2}x + 7$

Explanation:

Since this line has the y-intercept (0,7)

, we know that in the form y = mx+b

We can plug in the other intercept's coordinates for

and

to solve for

subtract

divide by

$\frac{-7}{2} = m$

The line is $y = -\frac{7}{2}x + 7$

Report an Error

View Tutors

Anjali
Certified Tutor

Delhi University, Bachelor of Science, Physics. Kumuan University, Master of Science, Physics.

View Tutors

Pankaj
Certified Tutor

University of Delhi, Electrical Engineer, Electrical Engineering. Columbia University in the City of New York, Master of Arts...

View Tutors

Bhavana
Certified Tutor

Indian Institute of Science Education and Research, Tirupati, Master's/Graduate, Physics and biology .

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Phoenix, Algebra Tutors in San Diego, French Tutors in Seattle, Biology Tutors in Dallas Fort Worth, MCAT Tutors in Dallas Fort Worth, Algebra Tutors in Phoenix, GRE Tutors in Chicago, Math Tutors in Boston, MCAT Tutors in New York City, GMAT Tutors in Miami

Popular Courses & Classes

GRE Courses & Classes in Seattle, Spanish Courses & Classes in Denver, LSAT Courses & Classes in Boston, GMAT Courses & Classes in Los Angeles, GRE Courses & Classes in Atlanta, SAT Courses & Classes in Chicago, ACT Courses & Classes in San Diego, Spanish Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Los Angeles, ISEE Courses & Classes in San Diego

Popular Test Prep

LSAT Test Prep in Boston, GMAT Test Prep in Boston, GRE Test Prep in Phoenix, ACT Test Prep in Boston, GRE Test Prep in Philadelphia, SAT Test Prep in Philadelphia, MCAT Test Prep in Denver, SAT Test Prep in Miami, ISEE Test Prep in San Diego, SAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : How to find the equation of a curve

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #1 : How To Find The Equation Of A Curve

Example Question #1 : How To Find The Equation Of A Curve

Example Question #1 : How To Find The Equation Of A Curve

Example Question #2 : How To Find The Equation Of A Curve

Example Question #3 : How To Find The Equation Of A Curve

Example Question #1 : How To Find The Equation Of A Curve

Example Question #2 : How To Find The Equation Of A Curve

Example Question #2 : How To Find The Equation Of A Curve

Example Question #2 : How To Find The Equation Of A Curve

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: