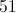We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Lower Level Quantitative : How to find the solution to an equation

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

Create An Account

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Solution To An Equation

What is the value of x in the equation?

$\dpi{100} \frac{200+50}{5}=x$

Possible Answers:

$\dpi{100} 25$

$\dpi{100} 5$

$\dpi{100} 50$

$\dpi{100} 100$

Correct answer:

$\dpi{100} 50$

Explanation:

First, add $\dpi{100} 200+50=250$ .

Next, divide $\dpi{100} 250\div 5=50$ .

So $\dpi{100} x=50$

Report an Error

Example Question #1 : Algebraic Concepts

Simplify.

-7x +4x-11-x+3

Possible Answers:

-4x+8

-4x-8

-4x-14

4x+8

Correct answer:

-4x-8

Explanation:

When simplifying an expression, you must combine like terms. There are two types of terms in this expression: “x’s” and whole numbers. Combine in two steps:

1) x’s: -7x+4x-x=-4x

2) whole numbers: -11+3=-8

The simplified expression is: -4x-8 .

Report an Error

Example Question #3 : How To Find The Solution To An Equation

Solve, when x=-2 .

$-6x^{2}+12x+3=$

Possible Answers:

Correct answer:

Explanation:

To solve, insert for each :

$-6(-2)^{2}+12(-2)+3=$

Simplify:

-6(4)-24+3=

-24-24+3=-45

*Common error: When solving this part of the equation always remember the order of operations (PEMDAS) and square the number in the () BEFORE multiplying!

Report an Error

Example Question #4 : How To Find The Solution To An Equation

Solve for .

$5x^{2}-14=6$

Possible Answers:

Correct answer:

Explanation:

$5(-2)^{2}-14=6$

Report an Error

Example Question #5 : Algebraic Concepts

Use the equations to answer the question.

3 + x=4

9+y=13

What is x+y ?

Possible Answers:

Correct answer:

Explanation:

First, you need to find what would make and true in their respective equations. equals 1 and equals 4. The next step is to add those together, which gives you 5.

Report an Error

Example Question #3 : Equations

What story best fits the expression $9\times3$ ?

Possible Answers:

Michelle had 3 stuffed animals and gave 1 away.

Nell bought 9 bags of candy with 3 pieces of candy in each bag.

Lisa had 9 pencils with two erasers each.

Jonah had 3 baseball cards, but after his friend gave him some, he had 12.

Correct answer:

Nell bought 9 bags of candy with 3 pieces of candy in each bag.

Explanation:

Nell's story fits best because if she bought 9 bags with 3 pieces each, that would be 27 total. This fits best with the $9\times 3=27$ equation.

Report an Error

Example Question #5 : Equations

What is equal to in this equation:

4x+5=13

Possible Answers:

Correct answer:

Explanation:

Find the number that makes the equation true. 2 works because when plugged in, the left side of the equation becomes 13, making the whole equation true.

Report an Error

Example Question #7 : Algebraic Concepts

Five more than a number is equal to $\frac{3}{5}$ of twenty-five . What is the number?

Possible Answers:

Correct answer:

Explanation:

From the question, we know that plus a number equals $\frac{3}{5}$ of . In order to find out what $\frac{3}{5}$ of is, multiply $\frac{3}{5}$ by $\frac{25}{1}$ .

$\frac{3}{5}\times\frac{25}{1}=\frac{75}{5}$ , or .

The number we are looking for needs to be five less than , or .

You can also solve this algebraically by setting up this equation and solving:

$5+x=\frac{3}{5}\times25$

5+x=15

Subtract from both sides of the equation.

x=10

Report an Error

Example Question #4 : Equations

Solve for .

2x-2=10

Possible Answers:

x=8

x=12

x=10

x=6

Correct answer:

x=6

Explanation:

To solve for , we want to isolate , or get it by itself.

2x-2=10

Add to both sides of the equation.

2x-2=10

2x=12

Now we need to divide both sides by the coefficient of , i.e. the number directly in front of the .

2x=12

x=6

Report an Error

Example Question #5 : Equations

Solve for .

18=3x+3

Possible Answers:

Correct answer:

Explanation:

First, subtract the three from both sides:

$18-3=3x+3\left ( -3\right )$

15=3x

Then, divide by three on both sides:

$\frac{15}{3}=\frac{3x}{3}$

5=x

Report an Error

View Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

View Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Phoenix, Chemistry Tutors in Philadelphia, Calculus Tutors in Atlanta, French Tutors in Houston, French Tutors in Dallas Fort Worth, LSAT Tutors in Dallas Fort Worth, Computer Science Tutors in Denver, LSAT Tutors in Seattle, Algebra Tutors in Philadelphia, Spanish Tutors in Phoenix

Popular Courses & Classes

GMAT Courses & Classes in Boston, SAT Courses & Classes in Boston, ACT Courses & Classes in Boston, Spanish Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Seattle, Spanish Courses & Classes in Boston, MCAT Courses & Classes in Boston, MCAT Courses & Classes in Los Angeles, ACT Courses & Classes in Houston, Spanish Courses & Classes in Seattle

Popular Test Prep

ISEE Test Prep in Denver, SAT Test Prep in Denver, ACT Test Prep in Houston, GRE Test Prep in Los Angeles, SSAT Test Prep in San Diego, SAT Test Prep in Boston, LSAT Test Prep in Boston, MCAT Test Prep in Atlanta, GRE Test Prep in San Diego, ISEE Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Lower Level Quantitative : How to find the solution to an equation

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

All ISEE Lower Level Quantitative Resources

Example Questions

Example Question #1 : How To Find The Solution To An Equation

Example Question #1 : Algebraic Concepts

Example Question #3 : How To Find The Solution To An Equation

Example Question #4 : How To Find The Solution To An Equation

Example Question #5 : Algebraic Concepts

Example Question #3 : Equations

Example Question #5 : Equations

Example Question #7 : Algebraic Concepts

Example Question #4 : Equations

Example Question #5 : Equations

All ISEE Lower Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: