All ISEE Middle Level Quantitative Resources
Example Questions
Example Question #1 : Range
Which is the greater quantity?
(A) The midrange of the data set
(B) The midrange of the data set
(A) is greater
(B) is greater
(A) and (B) are equal
It is impossible to determine which is greater from the information given
(A) is greater
The midrange of a data set is the mean of its least and greatest elements. The midrange of the first data set is 

Example Question #4 : Data Analysis
Set 
Set 

What is the range of values in set 
To find the range of a set of numbers, you do not even have to put them in order. You merely need to subtract the smallest value from the largest. Given the way of constructing set 



Smallest: 
Largest:
Therefore, the range is:
Example Question #2 : Data Analysis
The members of set 
For values of 


What is the range of set 
To find the range of a set of numbers, you do not even have to put them in order. You merely need to subtract the smallest value from the largest. Given the way that we construct set 


Smallest: 
Largest:
Therefore, the range is:
Example Question #3 : Data Analysis
Set 
The members of set 



So, for instance, set T contains 

What is the range of set 
We first need to determine the members of set 

Our largest value is 

Example Question #2 : Range
Given the below set of numbers find the range:
Range for a set of data is defined as the difference between the biggest and smallest number.
First we find the biggest number which is 15, we then subtract the smallest number in this set which is negative 2 as shown below:
Remember, when subtracting a negative number we must add the numbers.
Example Question #8 : Data Analysis
Given the below set of numbers, find the range:
In order to find the range, we must subtract the smallest number from the biggest number.
We must convert the fractions to have a common denominator which is 10.
Therefore, the range of this set is

Example Question #9 : Data Analysis
Given the below set of numbers, find the range:
In order to find the range, we must subtract the smallest number from the biggest number.
We must convert the fractions to have a common denominator which is 10.
Therefore, the range of this set is

Example Question #9 : Find Range
Find the range of the data set provided:

In order to answer this question correctly, we need to recall the definition of range:
Range: The range of a data set is the difference between the highest value and the lowest value in the set.
In order to find the range, we need to first organize the data from least to greatest to find the lowest and highest values:
Next, we can solve for the difference between the highest value and the lowest value:
The range for this data set is
Example Question #10 : Find Range
Find the range of the data set provided:

In order to answer this question correctly, we need to recall the definition of range:
Range: The range of a data set is the difference between the highest value and the lowest value in the set.
In order to find the range, we need to first organize the data from least to greatest to find the lowest and highest values:
Next, we can solve for the difference between the highest value and the lowest value:
The range for this data set is
Example Question #1 : Range
Find the range of the data set provided:

In order to answer this question correctly, we need to recall the definition of range:
Range: The range of a data set is the difference between the highest value and the lowest value in the set.
In order to find the range, we need to first organize the data from least to greatest to find the lowest and highest values:
Next, we can solve for the difference between the highest value and the lowest value:
The range for this data set is
Certified Tutor
All ISEE Middle Level Quantitative Resources













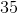

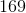






































![\frac{\begin{array}[b]{r}36\\ -\ 26\end{array}}{ \ \ \ \space 10}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/992027/gif.latex)






![\frac{\begin{array}[b]{r}27\\ -\ 11\end{array}}{ \ \ \ \space 16}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/992039/gif.latex)






![\frac{\begin{array}[b]{r}11\\ -\ 1\end{array}}{ \ \ \ \space 10}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/992085/gif.latex)




