The gray area represents the set of all elements that are in \(\displaystyle B\) but not in \(\displaystyle A\).

\(\displaystyle B\) is the set of integers that, when divided by 3, yield remainder 2. Therefore, we can eliminate 102 and 105, both multiples of 3, and 103, which, when divided by 3, yields remainder 1.

\(\displaystyle A\) is the set of integers that, when divided by 4, yield remainder 1. Since we do not want an element from this set, we can eliminate 101, but not 104. 

104 is the correct choice.

\(\displaystyle A \cap B\) is the intersection of sets \(\displaystyle A\) and \(\displaystyle B\) - that is, the set of all elements of \(\displaystyle U\) that are elements of both \(\displaystyle A\) and \(\displaystyle B\). We want all of the letters that fall in both circles, which from the diagram can be seen to be \(\displaystyle a\) and \(\displaystyle f\). Therefore, 

\(\displaystyle A \cap B = \left \{ a,f \right \}\)

\(\displaystyle \overline{A \cap B}\)  is the complement of \(\displaystyle A \cap B\) - the set of all elements in \(\displaystyle U\) not in \(\displaystyle A \cap B\). 

\(\displaystyle A \cap B\) is the intersection of sets \(\displaystyle A\) and \(\displaystyle B\) - that is, the set of all elements of \(\displaystyle U\) that are elements of both \(\displaystyle A\) and \(\displaystyle B\). Therefore, \(\displaystyle \overline{A \cap B}\) is the set of all elements that are not in both \(\displaystyle A\) and \(\displaystyle B\), which can be seen from the diagram to be all elements except \(\displaystyle a\) and \(\displaystyle f\). Therefore, 

\(\displaystyle \overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}\).

\(\displaystyle \overline{A\cup B}\) is the complement of \(\displaystyle A\cup B\) - the set of all elements in \(\displaystyle U\) not in \(\displaystyle A\cup B\).

\(\displaystyle A\cup B\) is the union of sets \(\displaystyle A\) and \(\displaystyle B\) - the set of all elements in either \(\displaystyle A\) or \(\displaystyle B\). Therefore, \(\displaystyle \overline{A\cup B}\) is the set of all elements in neither \(\displaystyle A\) nor \(\displaystyle B\), which can be seen from the diagram to be only one element - \(\displaystyle c\). Therefore, 

\(\displaystyle \overline{A\cup B} = \left \{ c\right \}\)

The number of students who play football or baseball can by finding the summer of the number of students who play football alone, baseball alone, baseball and football, and all three sports.

\(\displaystyle 30+20+3+3=56\)

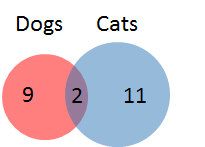
First, calculate the number of students with a dog:
\(\displaystyle 9+2=11\)

Next, subtract the number of students with a dog from the total number of students.

\(\displaystyle 30-11=19\)

We need to know the total number of possibilities, and the total number of ways to achieve our goal.

A standard die has 6 faces, so there are a total of 6 numbers that we could roll.

We want to roll a 1 or a 2, which means there are 2 ways that we can succeed (rolling a 1 or a 2).

Thus, we have a probability of success as \(\displaystyle \dpi{100} \frac{2}{6}\) which reduces to \(\displaystyle \dpi{100} \frac{1}{3}\).

The costs of the beverages will be as follows:

\(\displaystyle \begin{matrix} \textrm{4 Sodas}& \4 \times $1.29 = \$5.16 \\ \textrm{2 Iced Teas} & 2 \times \$1.39 = \$2.78 \\ \textrm{2 Coffees} &2 \times \$1.69 = \$3.38 \\ \textrm{1 Hot Tea} & \$1.59 \\ \textrm{1 Milk} & \$1.49 \end{matrix}\)

Add these amounts:

\(\displaystyle \begin{matrix} \; \$5.16\\ \; \; 2.78\\ \; \; 3.38\\ \; \; 1.59\\\; \; \underline{1.49}\\ \$14.40 \end{matrix}\)

20% of $14.40 is \(\displaystyle 14.40 \times 0.20 = 2.88\) , or $2.90 when rounded to the nearest dime. 

There were four days that saw a peak temperature of 75 degrees or greater:

Monday: 76 degrees

Tuesday: 80 degrees

Wednesday: 77 degrees

Friday: 78 degrees

The highest point on the line graph is located at Tuesday.