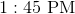Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : How to find the angle of a sector

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Angle Of A Sector

A giant clock has a minute hand four feet long. Since noon, the tip of the minute hand has traveled $10 \pi$ feet. What time is it now?

Possible Answers:

$1:45 \textrm{ PM}$

$12:45 \textrm{ PM}$

$1:30 \textrm{ PM}$

$1:15 \textrm{ PM}$

$1:20 \textrm{ PM}$

Correct answer:

$1:15 \textrm{ PM}$

Explanation:

The circumference of the path traveled by the tip of the minute hand over the course of one hour is:

$C = 2 \pi r = 2 \pi \cdot 4 = 8 \pi$ feet.

Since the tip of the minute hand has traveled $10 \pi$ feet since noon, the minute hand has made

$\frac{10 \pi }{8 \pi } = \frac{5}{4} = 1 \frac{1}{4}$ revolutions. Therefore, $1 \frac{1}{4}$ hours have elapsed since noon, making the time 1:15 PM.

Report an Error

Example Question #1 : How To Find The Angle Of A Sector

Inscribed angle

Figure NOT drawn to scale

Refer to the above diagram. $\overarc {ABC}$ is a semicircle. Evaluate $m \overarc {BCA}$ given $\measuredangle B=90^\circ$ .

Possible Answers:

$282^{\circ }$

$302^{\circ }$

$292^{\circ }$

$312^{\circ }$

Correct answer:

$312^{\circ }$

Explanation:

An inscribed angle of a circle that intercepts a semicircle is a right angle; therefore, $\angle B$ , which intercepts the semicircle $\overarc {ABC}$ , is such an angle. Consequently, $\bigtriangleup ABC$ is a right triangle, and $\angle A$ and $\angle C$ are complementary angles. Therefore,

$m \angle A + m \angle C = 90 ^{\circ }$

$y + \left ( \frac{y}{3}+2\right ) = 90$

$y + \frac{1}{3}y +2 = 90$

$\frac{4}{3}y +2 = 90$

$\frac{4}{3}y +2 - 2 = 90 - 2$

$\frac{4}{3}y = 88$

$\frac{3}{4} \cdot \frac{4}{3}y = \frac{3}{4} \cdot 88$

y = 66

$m \angle C = \left (\frac{y}{3}+ 2 \right ) ^{\circ }=\left ( \frac{66}{3}+ 2 \right )^{\circ }=( 22 + 2 )^{\circ }= 24^{\circ }$

Inscribed $\angle C$ intercepts an arc with twice its angle measure; this arc is $\overarc {AB}$ , so

$m \overarc {AB} = 2 \cdot m \angle C = 2 \cdot 24 ^{\circ } = 48 ^{\circ }$ .

The major arc corresponding to this minor arc, $\overarc {BCA}$ , has measure

$m \overarc {BCA} = 360 ^{\circ } - m \overarc {AB} = 360 ^{\circ } - 48^{\circ } = 312^{\circ }$

Report an Error

Example Question #1 : How To Find The Angle Of A Sector

Inscribed angle

Note: Figure NOT drawn to scale

Refer to the above diagram. $\overarc {ABC}$ is a semicircle. Evaluate $m \overarc {AB}$ .

Possible Answers:

$69^{\circ }$

$74 ^{\circ }$

$79 ^{\circ }$

$64 ^{\circ }$

Correct answer:

$74 ^{\circ }$

Explanation:

An inscribed angle of a circle that intercepts a semicircle is a right angle; therefore, $\angle B$ , which intercepts the semicircle $\overarc{ABC}$ , is such an angle. Consequently,

$m \angle B = 90 ^{\circ }$

4x-18 = 90

4x - 18 + 18 = 90 + 18

4x = 108

$4x \div 4 = 108 \div 4$

x = 27

$m \angle C = (x+10)^{\circ } = (27+10)^{\circ }= 37^{\circ }$

Inscribed $\angle C$ intercepts an arc with twice its angle measure; this arc is $\overarc{AB}$ , so

$m \widehat{AB} = 2 \cdot m \angle C = 2 \cdot 37 ^{\circ } = 74 ^{\circ }$ .

Report an Error

Example Question #2 : How To Find The Angle Of A Sector

Intercepted

In the above diagram, radius AO = 20 .

Calculate the length of $\overarc {AB}$ .

Possible Answers:

$32 \pi$

$40 \pi$

$8 \pi$

$16 \pi$

Correct answer:

$16 \pi$

Explanation:

Inscribed $\angle ACB$ , which measures $72 ^{\circ }$ , intercepts an arc with twice its measure. That arc is $\overarc {AB}$ , which consequently has measure

$72 ^{\circ } \times 2 = 144 ^{\circ }$ .

This makes $\overarc {AB}$ an arc which comprises

$\frac{144}{360} = \frac{144 \div 72}{360 \div 72} = \frac{2}{5}$

of the circle.

The circumference of a circle is $2 \pi$ multiplied by its radius, so

$C = 2 \pi r = 2\pi \cdot 20 = 40 \pi$ .

The length of $\overarc {AB}$ is $\frac{2}{5}$ of this, or $\frac{2}{5} \cdot 40 \pi = 16 \pi$ .

Report an Error

Example Question #2 : How To Find The Angle Of A Sector

Secant

Figure NOT drawn to scale.

The circumference of the above circle is 120. $\overarc{AB }$ and $\overarc{CD}$ have lengths 10 and 20, respectively. Evaluate .

Possible Answers:

t = 15

t = 24

t = 18

t = 30

Correct answer:

t = 15

Explanation:

The length of $\overarc{AB }$ comprises $\frac{10}{120} = \frac{1}{12}$ of the circumference of the circle. Therefore, its degree measure is $\frac{1}{12} \cdot 360 ^{\circ } = 30^{\circ }$ . Similarly, The length of $\overarc{CD}$ comprises $\frac{20}{120} = \frac{1}{6}$ of the circumference of the circle. Therefore, its degree measure is $\frac{1}{6} \cdot 360 ^{\circ } = 60 ^{\circ }$ .

If two secants are constructed to a circle from an outside point, the degree measure of the angle the secants form is half the difference of those of the arcs intercepted - that is,

$t = \frac{1}{2} ( m \overarc {CD} - m \overarc{AB})$

$t = \frac{1}{2} ( 60 - 30 ) = \frac{1}{2} \cdot 30 = 15$ .

Report an Error

Example Question #91 : Circles

Tangents

Figure NOT drawn to scale.

Refer to the above diagram. $\overarc{AB }$ and $\overarc{ABC}$ have lengths 80 and 160, respectively. Evaluate .

Possible Answers:

t = 66

t = 72

t = 60

t = 78

Correct answer:

t = 60

Explanation:

The circumference of the circle is the sum of the two arc lengths:

80 + 160 = 240

The length of $\overarc{AB }$ comprises $\frac{80}{240} = \frac{1}{3}$ of the circumference of the circle. Therefore, its degree measure is $\frac{1}{3} \cdot 360 ^{\circ } = 120 ^{\circ }$ . Consequently, $\overarc{ACB }$ is an arc of degree measure $360 ^{\circ } - 120 ^{\circ } = 240^{\circ }$ .

The segments shown are both tangents from to the circle. Consequently, the degree measure of the angle they form is half the difference of the angle measures of the arcs they intercept - that is,

$t = \frac{1}{2} ( m \overarc {ACB} - m \overarc{AB})$

$t = \frac{1}{2} ( 240 ^{\circ } - 120^{\circ }) = \frac{1}{2} \cdot 120^{\circ } = 60 ^{\circ }$

Report an Error

Example Question #3 : How To Find The Angle Of A Sector

Chords

Figure NOT drawn to scale.

The circumference of the above circle is 100. $\overarc{AB }$ and $\overarc{CD}$ have lengths 20 and 15, respectively. Evaluate .

Possible Answers:

t =72

t= 54

t = 81

t =63

Correct answer:

t =63

Explanation:

The length of $\overarc{AB }$ comprises $\frac{20}{100} = \frac{1}{5}$ of the circumference of the circle. Therefore, its degree measure is $\frac{1}{5} \cdot 360 ^{\circ } = 72 ^{\circ }$ . Similarly, The length of $\overarc{CD}$ comprises $\frac{15}{100} = \frac{3}{20}$ of the circumference of the circle. Therefore, its degree measure is $\frac{3}{20} \cdot 360 ^{\circ } = 54 ^{\circ }$ .

If two chords cut each other inside the circle, as $\overline{AC }$ and $\overline{BD}$ do, and one pair of vertical angles are examined, then the degree measure of each angle is half the sum of those of the arcs intercepted - that is,

$t = \frac{1}{2} ( m \overarc{AB}+ m \overarc {CD})$

$t = \frac{1}{2} ( 72 ^{\circ } + 54 ^{\circ })$

$t = \frac{1}{2} ( 126^{\circ })$

$t =63 ^{\circ }$

Report an Error

View Tutors

Myung Hee
Certified Tutor

Pukyung National University, Bachelor of Science, Japanese Studies. University of Padova, Master of Science, International Bu...

View Tutors

Dehlly
Certified Tutor

Universidad Nacional de Colombia, Bachelor in Business Administration, Mathematics and Statistics. Columbia University in th...

View Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Seattle, LSAT Tutors in Washington DC, GMAT Tutors in Washington DC, Computer Science Tutors in Phoenix, English Tutors in Houston, GMAT Tutors in San Francisco-Bay Area, Reading Tutors in Philadelphia, ACT Tutors in Atlanta, LSAT Tutors in San Francisco-Bay Area, Reading Tutors in Phoenix

Popular Courses & Classes

ISEE Courses & Classes in New York City, SSAT Courses & Classes in Seattle, LSAT Courses & Classes in Phoenix, LSAT Courses & Classes in Denver, SAT Courses & Classes in San Diego, Spanish Courses & Classes in Houston, GRE Courses & Classes in San Diego, LSAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Miami, MCAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

SSAT Test Prep in Philadelphia, ACT Test Prep in Seattle, SSAT Test Prep in Houston, MCAT Test Prep in Chicago, ISEE Test Prep in Atlanta, SAT Test Prep in Phoenix, SSAT Test Prep in Washington DC, GMAT Test Prep in Seattle, GRE Test Prep in Atlanta, LSAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : How to find the angle of a sector

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #1 : How To Find The Angle Of A Sector

Example Question #1 : How To Find The Angle Of A Sector

Example Question #1 : How To Find The Angle Of A Sector

Example Question #2 : How To Find The Angle Of A Sector

Example Question #2 : How To Find The Angle Of A Sector

Example Question #91 : Circles

Example Question #3 : How To Find The Angle Of A Sector

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: