Call Now to Set Up Tutoring:

(888) 888-0446

Linear Algebra : Gradients of the Determinant

Study concepts, example questions & explanations for Linear Algebra

Create An Account

All Linear Algebra Resources

4 Diagnostic Tests 108 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #71 : Linear Algebra

Which of the following expressions is one for the gradient of the determinant of an 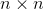$n \times n$ $\displaystyle n \times n$ matrix $\displaystyle A$?

Possible Answers:

$(adj(A))^{-1}$ $\displaystyle (adj(A))^{-1}$

$\mathbf{x}^{-1}A\mathbf{x}, (\|\mathbf{x}\|=1)$ $\displaystyle \mathbf{x}^{-1}A\mathbf{x}, (\|\mathbf{x}\|=1)$

$\displaystyle (adj(A))^T$

None of the other answers

Correct answer:

$\displaystyle (adj(A))^T$

Explanation:

The expression for the determinant of $\displaystyle A$ using co-factor expansion (along any row) is

$|A| = \sum_{i=1}^n(-1)^{i+j}A_{ij}M_{ij}$ $\displaystyle |A| = \sum_{i=1}^n(-1)^{i+j}A_{ij}M_{ij}$

In order to find the gradient of the determinant, we take the partial derivative of the determinant expression with respect to some entry $A_{kl}$ $\displaystyle A_{kl}$ in our matrix, yielding $(-1)^{k+l}M_{kl} = (adj(A))_{kl} = (adj(A))^T$ $\displaystyle (-1)^{k+l}M_{kl} = (adj(A))_{kl} = (adj(A))^T$.

Report an Error

View Linear Algebra Tutors

Alexander
Certified Tutor

Carnegie Mellon University, Bachelor of Science, Mathematics and Computer Science.

View Linear Algebra Tutors

Jonathan
Certified Tutor

University of California, Berkeley, Bachelor's, Data Science, Public Health.

View Linear Algebra Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

All Linear Algebra Resources

4 Diagnostic Tests 108 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Los Angeles, SSAT Tutors in New York City, Reading Tutors in Los Angeles, Chemistry Tutors in Washington DC, Computer Science Tutors in San Francisco-Bay Area, French Tutors in Houston, Computer Science Tutors in Seattle, Reading Tutors in Philadelphia, Spanish Tutors in Denver, GMAT Tutors in Washington DC

Popular Courses & Classes

GMAT Courses & Classes in Atlanta, GRE Courses & Classes in Los Angeles, ACT Courses & Classes in Phoenix, GMAT Courses & Classes in Washington DC, GMAT Courses & Classes in Chicago, Spanish Courses & Classes in New York City, SAT Courses & Classes in Atlanta, ACT Courses & Classes in Atlanta, ISEE Courses & Classes in Washington DC, ISEE Courses & Classes in Dallas Fort Worth

Popular Test Prep

GRE Test Prep in Miami, SAT Test Prep in Seattle, LSAT Test Prep in Dallas Fort Worth, ACT Test Prep in Houston, LSAT Test Prep in Denver, LSAT Test Prep in Philadelphia, GMAT Test Prep in Chicago, ACT Test Prep in Atlanta, GMAT Test Prep in Washington DC, GRE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Linear Algebra : Gradients of the Determinant

Study concepts, example questions & explanations for Linear Algebra

All Linear Algebra Resources

Example Questions

Example Question #71 : Linear Algebra

All Linear Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: