All Linear Algebra Resources
Example Questions
Example Question #1 : Vector Vector Product
Compute , where
Not possible
Before we compute the product of , and , we need to check if it is possible to take the product. We will check the dimensions. is , and is , so the dimensions of the resulting matrix will be . Now let's compute it.
Example Question #1 : Vector Vector Product
Find the vector-vector product of the following vectors.
It's not possible to multiply these vectors
Example Question #2 : Vector Vector Product
Calculate , given
By definition,
.
Example Question #3 : Vector Vector Product
What is the physical significance of the resultant vector , if ?
is orthogonal to both and .
is the projection of onto .
lies in the same plane that contains both and .
is a scalar.
is orthogonal to both and .
By definition, the resultant cross product vector (in this case, ) is orthogonal to the original vectors that were crossed (in this case, and ). In , this means that is a vector that is normal to the plane containing and .
Example Question #133 : Matrices
Example Question #3 : Vector Vector Product
Example Question #135 : Matrices
Example Question #136 : Matrices
Example Question #137 : Matrices
Example Question #138 : Matrices
Certified Tutor
Certified Tutor
All Linear Algebra Resources




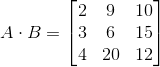









![A=[1 \ 2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/727325/gif.latex)













![\textbf{A} \times \textbf{B} = \begin{vmatrix} \hat{i}& \hat{j}&\hat{k} \\ 4& -2& 0\\ 1& 3& 0 \end{vmatrix} =\hat{i}(0)-\hat{j}(0)+\hat{k}[4(3)-1(-2)] = 14 \hat{k}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/800856/gif.latex)


























































