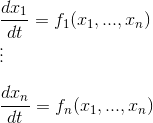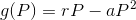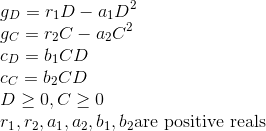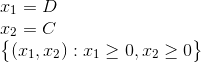Math Modeling : Dynamic Models
Study concepts, example questions & explanations for Math Modeling
All Math Modeling Resources
Example Questions
Example Question #1 : Dynamic Models
There are two similar species of monkey that inhabit the same forest. The intrinsic growth rate is 4% for species A and 7% for species B. The capacity of the forest is estimated at 125,000 specie A monkeys and 450,000 species B monkeys. Poaching these monkeys over the last 100 years has caused for a decline in each species. Species A has a population of 4,000 and species B, a population of 80,000. Use a discrete model to project the population growth with a time step of several years. How large a time step can be used to maintain a continuous time model with an equivalent qualitative behavior?
Assume 
Identify the known information and the dynamical system.
The dynamical system equation is:
From here solve by using the Euler Method for a discrete time dynamical system.
Now formulate the model
Now transform these equations into a set of difference equations.
Assume
where 
The time step 
Using computer implementation of the Euler Method on the population of species B monkeys the following graph is produced.
It is seen that 
Example Question #1 : Intro To Dynamic Models
In a meadow there are two types of wild flowers growing, a green floor crawler and yellow daisies. The more desirable flower is the yellow daisy as they can be picked and sold for bouquets. The yellow daisies are also the more slow growing flower of the two. The green floor crawlers grow more rapidly and consume more of the meadow land. Yellow daisies compete with the green flower crawlers by growing taller and shading the crawlers new growth. The yellow daisies are also more resistant to certain types of bugs. Can these two types of flowers coexist on one portion of the meadow, or will one over run the other, driving it to extinction?
Both flowers will thrive.
The Yellow Daisies will go extinct.
Both flower will coexist.
The steady state analysis cannot answer the question.
The Green Floor Crawler will go extinct.
The steady state analysis cannot answer the question.
Since there is competition between the two differing species of flowers, the growth rate function is,
where 
Now identify the question as a dynamic model in steady state.
In other words,
From here, identify what is known about the problem in mathematical terms.
To answer the question determine whether 
To formulate the model let
where the steady state equations are as follows.
For the particular problem, the points on interests are at those where the two functions intersect.
and the intersection of
Using Cramer's rule to solve results in the following.
and when the question of coexistence is ask it is found that,
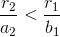
Which after further examination learns to the conclusion that the steady state analysis cannot answer the question.
All Math Modeling Resources
