All Physical Chemistry Resources
Example Questions
Example Question #1 : Gases
A researcher places a closed piston container at room temperature. He places a Bunsen burner at the bottom of the container and observes that the piston moves up. What can best explain this phenomenon?
The volume of the gas increased because of Boyle’s Law
The pressure of the gas decreased because of Charles’ Law
The volume of the gas increased because of Charles’ Law
The pressure of the gas decreased because of Boyle’s Law
The volume of the gas increased because of Charles’ Law
There are three main gas laws. Avogadro’s law states that the moles of a gas is directly proportional to the volume (under constant pressure and temperature). Boyle’s law states that the pressure of the gas is inversely proportional to the volume (under constant moles and temperature). This means that the pressure decreases proportionally when the volume increases. Charles’ law states that the temperature is directly proportional to the volume (under constant moles and pressure). The question states that the piston moves up. This means that the volume of the gas is expanding inside and pushing the piston up to make room for the expanding gas. The gas expansion occurs due to increased temperature (Charles’ law).
Example Question #1 : Gas Laws
At constant temperature and moles, which of the following is true regarding pressure and volume of a gas?
Pressure and volume have an exponential relationship with a negative correlation
Pressure and volume have an exponential relationship with a positive correlation
Pressure and volume are independent of each other
Pressure and volume have a linear relationship with a positive correlation
Pressure and volume have a linear relationship with a positive correlation
First, we need to figure out which gas law is applicable here. The question states that temperature and moles are constant. This means that we are dealing with Boyle’s law, which states that pressure is inversely proportional to volume. Inversely proportional means that the pressure decreases as volume increases and vice versa. Note that the relationship is still linear (change in one variable causes a proportional change in the other variable), but the two variables have a negative correlation. Positive correlation means increasing or decreasing a variable would also increase or decrease the other variable, respectively.
Example Question #1 : Gases
According to __________ law, increasing temperature will __________ volume at constant pressure and constant moles.
Charles’ . . . decrease
Boyle’s . . . increase
Boyle’s . . . decrease
Charles’ . . . increase
Charles’ . . . increase
Recall that Charles’ law defines the relationship between temperature and volume at constant pressure and constant moles. The law states that the two variables are directly proportional to each other. This means that increasing or decreasing temperature will have the same effect on volume. This makes sense because increasing the temperature increases the kinetic energy of the particles. This makes it easier for particles to move away from each other and expand, which results in an increase in volume.
Example Question #3 : Gases
An unknown gas is being analyzed in lab. You place 



Chlorine
Oxygen
Nitrogen
Argon
Oxygen
To solve this question we need to use the ideal gas law equation:
Above, 







Rearrange the ideal gas law and solve for 
The question states that you place one gram of gas in the container. Since we know the moles, we can solve for the molecular weight of the gas and figure out its identity from the molecular weight.
The molecular weight of oxygen gas, 

Example Question #2 : Gases
A sample of argon gas at a pressure of 0.959atm and a temperature of 
The argon gas, as the problem states, is under constant temperature with varying volume and pressure, so we need to use Boyle's Law:
We are given the initial pressure, the initial volume, and the final pressure, and need to solve for the final volume. Therefore, we can rearrange Boyle's law to be as follows:
Plug in known values and solve.
Example Question #6 : Gases
A sample of methane gas at a pressure of 0.723atm and a temperature of 
The methane gas, as the problem states, is under constant temperature with varying volume and pressure, so we need to use Boyle's Law:
We are given the initial pressure, the initial volume, and the final volume and need to solve for the final pressure. Therefore, we can rearrange Boyle's law to be as follows:
Plug in known values and solve.
Example Question #1 : Real And Ideal Gases
Given the ideal gas law:
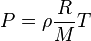
Where 




Based on the Ideal gas law, which of the following are true?
I. Pressure and volume are inversely proportional
II. Pressure and density are inversely proportional
III. Pressure and temperature are directly proportional
IV. Density and temperature are inversely proportional
V. R and M are inversely proportional
III, IV, V
I, III
I, III, IV
II, III, V
I, II, III, IV, V
I, III, IV
Condition I is true. Pressure and volume are inversely proportional. The ideal gas law with volume can be rederived to show this:
We introduce an expression for moles:
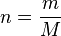
Where 


Rearranging (1) to solve for 
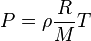
We get:

Finally, we use the following for density, where 
The masses cancel out and we have the ideal gas law expressed with volume and moles.
Condition II is false. It is clear from the equation that pressure and density are directly proportional.
Condition III is true because it is clear from the equation that temperature and pressure are directly proportional.
Condition IV is true because density and temperature are on the same side of the equation in the numerator, so the must be inversely proportional.
Condition V is false because the ideal gas constant and molar mass can be rearranged to be on opposite sides of the equation and in the numerator.
Example Question #2 : Gases
Under which conditions do gases deviate from ideality?
I. Low temperature
II. High temperature
III. Low pressure
IV. High pressure
V. Gases always behave ideally
V only
II and IV
II and III
I and III
I and IV
I and IV
Gases deviate from ideal conditions at low temperature and high pressure. This because the postulates of the kinetic molecular theory of gasses ignore the volume of the molecules and all interactions between gas molecules. However, neither are true for real gasses. As the temperature increases, the kinetic energy of the particles can overcome the intermolecular forces of attraction or repulsion between the molecules. At high pressures, and subsequently low volume, the distance between molecules becomes shorter, and therefore intermolecular forces become significant. So, ideal conditions are when the distance between molecules is great, and the energy each molecule has is much greater in relative magnitude to the intermolecular forces. This occurs when the pressure is low, and the temperature is high.
Example Question #1 : Real And Ideal Gases
Given the van der Waals Equation:
Which statement accurately identifies and explains the corrections that van der Waals made to the ideal gas law, where the first correction is the 

The first correction corrects for volume of molecules by increasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by decreasing pressure as volume increases and number of molecules increases.
The first correction corrects for volume of molecules by increasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by increasing pressure as volume decreases and number of molecules increases.
The first correction corrects for volume of molecules by decreasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by decreasing pressure as volume decreases and number of molecules increases.
The first correction corrects for volume of molecules by increasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by increasing pressure as volume increases and number of molecules increases.
The first correction corrects for volume of molecules by decreasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by increasing pressure as volume increases and number of molecules increases.
The first correction corrects for volume of molecules by decreasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by decreasing pressure as volume decreases and number of molecules increases.
All the statements say similar things, but only one correctly identifies the resulting change to volume and pressure. Let's break things down by the correction.
Correction 1:
The correction decreases the volume, since it is subtracting 
Correction 2:
Since we are subtracting 



All Physical Chemistry Resources

































