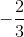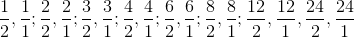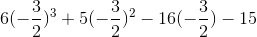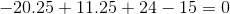To find the potential rational zeros by using the Rational Zero Theorem, first list the factors of the leading coefficient and the constant term:

Constant 24: 1, 2, 3, 4, 6, 8, 12, 24

Leading coefficient 2: 1, 2

Now we have to divide every factor from the first list by every factor of the second:

Removing duplicates [for example, and are both equivalent to 1] gives us the following list:

The only choice not on this list is .

The potential zeros must have a factor of -15 as their numerator and a factor of 6 as their denominator. This eliminates  as a possibility since 6 is not a factor of -15.

Now we need to test which of these values actually give zero when plugged into the polynomial.

First, :

Now :

Finally :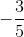

Since this one doesn't give us zero, it is not a solution of the polynomial.

To use Rational Zeros Theorem, take all factors of the constant term and all factors of the leading coefficient.  That gives you:

Constant Term = 12, so Factors: 1, 2, 3, 4, 6, 12

Leading Coefficient = 3, so Factors: 1, 3

Then divide every number from the first list by every number from the second -- keeping in mind that both positive and negative values are possible. Of course, since this is a multiple-choice question you can also use process-of-elimination to get rid of any values that wouldn't be possible from such division. Note that the only prime factors you have are 2 and 3, meaning that there is no way to produce a 5 or 7. That eliminates (or at least makes very suspect) several choices, leaving the choice:

If you perform division from the two lists you should see how you can arrive at each value from this choice: dividing 12 by 3 would give you 4 (or negative 4, again as both + and - values are possible); dividing 2 by 3 would give you , and dividing 2 by 1 or 6 by 3 would give you 2. Therefore this choice only includes possible zeros.

To use Rational Zeros Theorem, express a polynomial in descending order of its exponents (starting with the biggest exponent and working to the smallest), and then take the constant term (here that's 6) and the coefficient of the leading exponent (here that's 4) and express their factors:

Constant: 6 has as factors 1, 2, 3, and 6

Coefficient: 4 has as factors 1, 2, and 4

Then all possible rational zeros must be formed by dividing a factor from the Constant list by a factor from the Coefficient list (and note that the results should be considered as both positive and negative values).

Here if you then look at the answer choices, note that since the divisor - which must be a factor from the Coefficient list of 1, 2, and 4 - cannot then be a multiple of 3, you know that  is not a possible zero of this polynomial

To apply Rational Zero Theorem, first organize a polynomial in descending order of its exponents.  Then take the constant term and the coefficient of the highest-valued exponent and list their factors:

Constant: 2 has factors of 1 and 2

Coefficient: 2 has factors of 1 and 2

Then the potential rational zeros need to be formed by dividing a factor from the Constant list by a factor from the Coefficient list. Here you only have 1s and 2s, so your options are 1, 2, and 1/2 (and note that both positive and negative values will work). There is no way to get to 1/4, meaning that that is the correct answer.