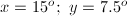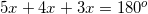All Precalculus Resources
Example Questions
Example Question #1 : Pre Calculus
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by 
Then by Hardy-Weinberg:



Which statement discribes the graph that would appropriately represents the above relation?
Curved line passing through the point
Straight line passing through the point
Parabola opening up passing through the point
Straight line passing through the point
Straight line passing through the point
The equation can be reduced by taking the square root of both sides.


As a simple test, all other values when substituted into the original equation fail. However, 

Example Question #1 : Graphing Functions
What is the y-intercept of the following equation?
The y-intercept can by found by solving the equation when x=0. Thus,
Example Question #2 : Graphing Functions
Determine the y intercept of 

In order to determine the y-intercept of 
Solving for y, when x is equal to zero provides you with the y coordinate for the intercept. Thus the y-intercept is 
Example Question #3 : Graphing Functions
What is the 

To find the 


Substituting 
Therefore, our 

Example Question #4 : Graphing Functions
What is the value of the 

The graph does not have a 
To find the 



Example Question #1 : Symmetry
If 

Even Symmetry
Odd Symmetry
No Symmetry
Symmetry across the line y=x
Even Symmetry
The definition of even symmetry is if
Example Question #2 : Graphing Functions
If 

Symmetry across the line y=x
Even symmetry
Odd symmetry
No symmetry
Odd symmetry

Example Question #1 : Angles
The angles are supplementary, therefore, the sum of the angles must equal 
Example Question #3 : Graphing Functions
Are 

Yes
Not enough information
No
Yes
Since supplementary angles must add up to 
Example Question #1 : Angles
The angles containing the variable 
Because 
Certified Tutor
All Precalculus Resources





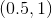
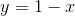



































 .
.









 and
and  .
.