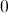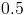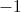We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Derivatives

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Pre Calculus

The function f(x) is such that

f'(0) = 0

When you take the second derivative of the function f(x) , you obtain

f''(x) = x^2

What can you conclude about the function at x=0 ?

Possible Answers:

The point is an absolute maximum.

The point is an absolute minimum.

The point is an inflection point.

The point is a local maximum.

The point is a local minimum.

Correct answer:

The point is an inflection point.

Explanation:

We have a point at which $f^{'}(x)=0$ . We know from the second derivative test that if the second derivative is negative, the function has a maximum at that point. If the second derivative is positive, the function has a minimum at that point. If the second derivative is zero, the function has an inflection point at that point.

Plug in 0 into the second derivative to obtain

f''(0)=0

So the point is an inflection point.

Report an Error

Example Question #1 : Pre Calculus

Consider the function

f(x)=x^2-x

Find the maximum of the function on the interval $\left [ 0,1 \right ]$ .

Possible Answers:

-0.5

0.5

Correct answer:

Explanation:

Notice that on the interval $\left [ 0,1 \right ]$ , the term $\ x^{2}$ is always less than or equal to . So the function is largest at the points when x^2=x . This occurs at x=0 and x=1 .

Plugging in either 1 or 0 into the original function f(x) yields the correct answer of 0.

Report an Error

Example Question #1 : Introductory Calculus

In what -intervals are the relative minimum and relative maximum for the function below?

f(x)=x^3-3x^2-4x

Possible Answers:

$\textup{There are no relative extrema}$

$\textup{Relative maximum in}\ \left ( -1,0\right )\textup{and a relative minimum in}\ \left ( 0,4\right )$

$\textup{Relative maximum in}\ \left ( -4,0\right )\textup{and a relative minimum in}\ \left ( 0,1\right )$

$\textup{Relative minimum in}\ \left ( -1,0\right )\textup{and a relative maximum in}\ \left ( 0,4\right )$

$\textup{Relative minimum in}\ \left ( -4,0\right )\textup{and a relative maximum in}\ \left ( 0,1\right )$

Correct answer:

$\textup{Relative maximum in}\ \left ( -1,0\right )\textup{and a relative minimum in}\ \left ( 0,4\right )$

Explanation:

A cubic function will have at most one relative minimum and one relative maximum. We can determine the zeros be factoring at x=-1,0,4 . From then we only need to determine if the graph is positive or negative in-between the zeros.

The graph is positive between and (plug in x=-0.5 ) and negative between 0 and 4 (plug in x=1 ). This can also be seen from the graph.

Wolframalpha--graph_of_y__x3-3x2-4x_from_x__-5_to_x__5_y__-15_to_y15--2014-12-19_0045

Report an Error

Example Question #1 : Derivatives

What is the minimum of the function f(x)=x^2-10x+26 ?

Possible Answers:

(7,3)

(5,1)

(4,0)

(6,2)

Correct answer:

(5,1)

Explanation:

The vertex form of a parabola is:

f(x)=a(x-h)^2+k

where {}(h,k) is the vertex of the parabola.

The function for this problem can be simplified into vetex form of a parabola:

f(x)=(x-5)^2+1 ,

with a vertex at (5,1) .

Since the parabola is concave up, the minimum will be at the vertex of the parabola, which is at (5,1) .

Report an Error

Example Question #1 : Rate Of Change Problems

Find the average rate of change of the function y=2e^x over the interval from x=0 to x=2 .

Possible Answers:

e^2-1

e^2

1-e^2

e(e-1)

Correct answer:

e^2-1

Explanation:

The average rate of change will be found by $\frac{f(2)-f(0)}{2-0}$ .

Here, f(2)=2e^2 , and f(0)=2e^0=2(1)=2 .

Now, we have $\frac{2e^2-2}{2-0}=\frac{2e^2-2}{2}=e^2-1$ .

Report an Error

Example Question #2 : Rate Of Change Problems

Let a function be defined by f(x)=-ln(x+1) .

Find the average rate of change of the function over [0,4] .

Possible Answers:

$ln\frac{-5}{4}$

$\frac{ln5}{4}$

$-\frac{ln5}{4}$

$-ln\frac{5}{4}$

Correct answer:

$-\frac{ln5}{4}$

Explanation:

We use the average rate of change formula, which gives us $\frac{f(4)-f(0)}{4-0}$ .

Now f(4)=-ln(4+1)=-ln5 , and f(0)=-ln(0+1)=-ln1=0 .

Therefore, the answer becomes $\frac{-ln5-0}{4-0}=-\frac{ln5}{4}$ .

Report an Error

Example Question #1 : Rate Of Change Problems

Suppose we can model the profit, , in dollars from selling items with the equation P(x)=3x^2-4x+2 .

Find the average rate of change of the profit from x=1 to x=4 .

Possible Answers:

Correct answer:

Explanation:

We need to apply the formula for the average rate of change to our profit equation. Thus we find the average rate of change is $\frac{P(4)-P(1)}{4-1}$ .

Since P(4)=3(4)^2-4(4)+2=3(16)-16+2=48-16+2=34 , and P(1)=3(1)^2-4(1)+2=3(1)-4+2=3-4+2=1 , we find that the average rate of change is $\frac{34-1}{4-1}=\frac{33}{3}=11$ .

Report an Error

Example Question #2 : Rate Of Change Problems

Let the profit, , (in thousands of dollars) earned from producing items be found by P(x)=2x^2-6x+25 .

Find the average rate of change in profit when production increases from 4 items to 5 items.

Possible Answers:

$\frac{4}{3}$

Correct answer:

Explanation:

Since P(5)=2(5)^2-6(5)+25 , we see that this equals 2(25)-30+25=50-30+25=20+25=45 . Now let's examine P(4) . P(4)=2(4)^2-6(4)+25=2(16)-24+25 which simplifies to .

Therefore the average rate of change formula gives us $\frac{f(5)-f(4)}{5-4}=\frac{45-33}{5-4}=\frac{12}{1}=12$ .

Report an Error

Example Question #2 : Rate Of Change Problems

Suppose that a customer purchases dog treats based on the sale price , where D(p)=15-p^2+p , where $1\leq p\leq3$ .

Find the average rate of change in demand when the price increases from $2 per treat to $3 per treat.

Possible Answers:

Correct answer:

Explanation:

D(3)=15-9+3=6+3=9

D(2)=15-4+2=13

Thus the average rate of change formula yields $\frac{9-13}{3-2}=\frac{-4}{1}=-4$ .

This implies that the demand drops as the price increases.

Report an Error

Example Question #4 : Rate Of Change Problems

A college freshman invests $100 in a savings account that pays 5% interest compounded continuously. Thus, the amount saved after years can be calculated by $A(t)=100e^{0.05t}$ .

Find the average rate of change of the amount in the account between t=0 and t=3 , the year the student expects to graduate.

Possible Answers:

$-\$5.39$

$\$38.73$

$\$5.39$

$\$38.39$

Correct answer:

$\$5.39$

Explanation:

$A(3)=100e^{0.05*3}=100e^{0.15}\approx \$116.18$ .

$A(0)=100e^{0.05*0}=100e^{0}=\$100.00$ .

Hence, the average rate of change formula gives us $\frac{A(3)-A(0)}{3-0}=\frac{\$116.18-\$100.00}{3-0}=\frac{\$16.18}{3}\approx \$5.39$ .

Report an Error

View Pre-Calculus Tutors

Dalton
Certified Tutor

University of Massachusetts Amherst, Doctor of Philosophy, Mathematics.

View Pre-Calculus Tutors

John
Certified Tutor

Arizona State University, Bachelor of Science, Microbiology.

View Pre-Calculus Tutors

Vandana
Certified Tutor

Jawaharlal Nehru Technological University, Bachelor of Technology, Civil Engineering. Florida International University, Maste...

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Denver, Reading Tutors in Philadelphia, Physics Tutors in Dallas Fort Worth, SAT Tutors in Chicago, Chemistry Tutors in San Francisco-Bay Area, ISEE Tutors in Los Angeles, English Tutors in Washington DC, ISEE Tutors in Phoenix, SAT Tutors in San Diego, ISEE Tutors in Chicago

Popular Courses & Classes

GMAT Courses & Classes in Miami, LSAT Courses & Classes in New York City, MCAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Seattle, SAT Courses & Classes in Denver, GRE Courses & Classes in San Diego, GMAT Courses & Classes in Washington DC, SSAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Washington DC, GMAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

LSAT Test Prep in Philadelphia, SSAT Test Prep in Miami, GRE Test Prep in San Diego, SSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Miami, GMAT Test Prep in Los Angeles, SSAT Test Prep in San Diego, ISEE Test Prep in New York City, ISEE Test Prep in Miami, LSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Derivatives

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #1 : Pre Calculus

Example Question #1 : Pre Calculus

Example Question #1 : Introductory Calculus

Example Question #1 : Derivatives

Example Question #1 : Rate Of Change Problems

Example Question #2 : Rate Of Change Problems

Example Question #1 : Rate Of Change Problems

Example Question #2 : Rate Of Change Problems

Example Question #2 : Rate Of Change Problems

Example Question #4 : Rate Of Change Problems

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: