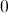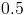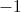All Precalculus Resources
Example Questions
Example Question #1 : Pre Calculus
The function 
When you take the second derivative of the function 
What can you conclude about the function at 
The point is a local maximum.
The point is an absolute maximum.
The point is an inflection point.
The point is a local minimum.
The point is an absolute minimum.
The point is an inflection point.
We have a point at which 
Plug in 0 into the second derivative to obtain
So the point is an inflection point.
Example Question #3 : Pre Calculus
Consider the function
Find the maximum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90593/gif.latex)
Notice that on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90594/gif.latex)





Plugging in either 1 or 0 into the original function 
Example Question #1 : Derivatives
In what 
A cubic function will have at most one relative minimum and one relative maximum. We can determine the zeros be factoring at 
The graph is positive between 




Example Question #15 : Pre Calculus
What is the minimum of the function 
The vertex form of a parabola is:
where 
The function for this problem can be simplified into vetex form of a parabola:

with a vertex at 
Since the parabola is concave up, the minimum will be at the vertex of the parabola, which is at 
Example Question #1 : Introductory Calculus
At what value of 

There is no hole
To find discontinuity we need to look at where the denominator of the function is equal to zero. Looking at our function,

we need to set the denominator equal to zero and solve for 
When 

Therefore 
Example Question #192 : Pre Calculus
What is the

The limit does not exist
Means to find the limit of the function as 






Example Question #1 : Introductory Calculus
What is the

The limit does not exist
We first need to simplify the function, we can do this by factoring the numerator and denominator.
If we plug in 3 into the simplified function, we get:
Example Question #2 : Introductory Calculus
What is the

Substituting 

Example Question #3 : Limits
Evaluate the following:
limit does not exist
When evaluating limits at infinity there are three rules to keep in mind:
- If the degree of the highest exponent in the numerator is equal to the degree of the highest exponent in the denominator, then the limit is equal to the ratio of the coefficient of the highest exponent in the numerator over the coefficient of the highest exponent in the denominator. Make sure to include signs.
- If the degree of the highest exponent in the numerator is less than the degree of the highest exponent in the denominator, the limit = 0.
- If the degree of the highest exponent in the numerator is greater than the degree of the higest exponent in the denominator, divide the highest power in the numerator by the highest power in the denominator and substitute for inifity. You will either subsitute for positive or negative infinity based on what the questions asks you to evaluate the limit at.
In this case, the degree is higher in the numerator than the denominator (rule #3). Hence, you need to divide the highest powers and evaluate.
Evaluate 
Answer: limit =
Example Question #4 : Limits
Evaluate the following:
When evaluating limits at infinity there are three rules to keep in mind:
- If the degree of the highest exponent in the numerator is equal to the degree of the highest exponent in the denominator, then the limit is equal to the ratio of the coefficient of the highest exponent in the numerator over the coefficient of the highest exponent in the denominator. Make sure to include signs.
- If the degree of the highest exponent in the numerator is less than the degree of the highest exponent in the denominator, the limit = 0.
- If the degree of the highest exponent in the numerator is greater than the degree of the higest exponent in the denominator, divide the highest power in the numerator by the highest power in the denominator and substitute for inifity. You will either subsitute for positive or negative infinity based on what the questions asks you to evaluate the limit at.
In this case, the both the numerator and denominator have the highest degree of an exponent of 4 (rule #1). Hence, you need to compare the ratio of the coefficients.
Answer: limit =
All Precalculus Resources