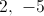Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Exponents and the Distributive Property

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Use Foil

Factor 2x² - 5x – 12

Possible Answers:

(x - 4) (2x + 3)

(x + 4) (2x + 3)

(x – 4) (2x – 3)

Correct answer:

(x - 4) (2x + 3)

Explanation:

Via the FOIL method, we can attest that x(2x) + x(3) + –4(2x) + –4(3) = 2x² – 5x – 12.

Report an Error

Example Question #1 : How To Use Foil

x > 0.

Quantity A: (x+3)(x-5)(x)

Quantity B: (x-3)(x-1)(x+3)

Possible Answers:

The two quantities are equal

Quantity B is greater

Quantity A is greater

The relationship cannot be determined from the information given

Correct answer:

Quantity B is greater

Explanation:

Use FOIL:

(x+3)(x-5)(x) = (x² - 5x + 3x - 15)(x) = x³ - 5x² + 3x² - 15x = x³ - 2x² - 15x for A.

(x-3)(x-1)(x+3) = (x-3)(x+3)(x-1) = (x² + 3x - 3x - 9)(x-1) = (x² - 9)(x-1)

(x² - 9)(x-1) = x³ - x² - 9x^₊ 9 for B.

The difference between A and B:

(x³ - 2x² - 15x) - (x³ - x² - 9x^₊ 9) = x³ - 2x² - 15x - x³ + x² + 9x - 9

= - x² - 4x - 9. Since all of the terms are negative and x > 0:

A - B < 0.

Rearrange A - B < 0:

A < B

Report an Error

Example Question #1 : Exponents And The Distributive Property

Solve for all real values of $\small x$ .

x^3+5x^2-10x=2x^2

Possible Answers:

$2,\ 5$

$0,\ 2,\ 5$

$0,\ 2,\ -5$

$2,\ -5$

Correct answer:

$0,\ 2,\ -5$

Explanation:

x^3+5x^2-10=2x^2

First, move all terms to one side of the equation to set them equal to zero.

x^3+5x^2-2x^2-10x=0

x^3+3x^2-10x=0

All terms contain an $\small x$ , so we can factor it out of the equation.

x(x^2+3x-10)=0

Now, we can factor the quadratic in parenthesis. We need two numbers that add to $\small 3$ and multiply to $\small -10$ .

$-2*5=-10\ \text{and}\ -2+5=3$

x(x-2)(x+5)=0

We now have three terms that multiply to equal zero. One of these terms must equal zero in order for the product to be zero.

$\begin{matrix} x=0 & x-2=0 &x+5=0 \\ x=0 & x=2 & x=-5 \end{matrix}$

Our answer will be $\small x=0,2,-5$ .

Report an Error

Example Question #1 : Exponents And The Distributive Property

Simplify: $(2x+3)^{2}$

Possible Answers:

$4x^{2}+9$

$4x^{2}-9$

$4x^{2}+12x+9$

$5x^{2}$

$4x^{2}+6x+9$

Correct answer:

$4x^{2}+12x+9$

Explanation:

In order to simplify this expression, you need to use the FOIL method. First rewrite the expression to look like this: (2x+3)(2x+3)

Next, multiply your first terms together: $2x\times2x =4x^{2}$

Then, multiply your outside terms together: $2x\times3=6x$

Then, multiply your inside terms together: $3\times2x=6x$

Lastly, multiply your last terms together: $3\times3=9$

Together, you have $4x^{2}+6x+6x+9$

You can combine your like terms, 6x+6x , to give you the final answer: $4x^{2}+12x+9$

Report an Error

Example Question #5 : Exponents And The Distributive Property

Use FOIL to simplify the following product:

(x+9)(x-7)

Possible Answers:

x^2+7x+54

x^2+2x-63

x^2-63

x^2+11x+63

7x^2-9x

Correct answer:

x^2+2x-63

Explanation:

Use the FOIL method (first, outside, inside, last) to find the product of:

(x+9)(x-7)

First: $x\cdot x=x^2$

Outside: $-7\cdot x=-7x$

Inside: $9\cdot x=9x$

Last: $-7\cdot 9=-63$

Sum the products to find the polynomial:

x^2-7x+9x-63

x^2+2x-63

Report an Error

Example Question #6 : Exponents And The Distributive Property

Simplify:

$2(x^{2}+x)(x-1)$

Possible Answers:

$2x^{3} -2x$

$2x^{3} -x$

$2x^{3}+4x^{2}-2x$

$2x^{3}+2x^{2}-2x-1$

$2x^{3}+2x^{2}-2x$

Correct answer:

$2x^{3} -2x$

Explanation:

To solve this problem, use the FOIL method. Start by multiplying the First term in each set of parentheses: $x^{2} \cdot x =x^{3}$

Then multiply the outside terms: $x^{2}\cdot (-1) =-x^{2}$

Next, multiply the inside terms: $x \cdot x= x^{2}$

Finally, multiply the last terms: $x\cdot (-1) = -x$

When you put the pieces together, you have $2(x^{3} -x^{2} +x^{2}-x)$ . Notice that the middle terms cancel each other out, and you are left with $2(x^{3} -x)$ . When you distribute the two, you reach the answer: $2x^{3} -2x$

Report an Error

Example Question #2 : Exponents And The Distributive Property

If (x-3)^2=25 , which of the following could be the value of ?

Possible Answers:

Correct answer:

Explanation:

(x-3)^2=25

Take the square root of both sides.

$x-3=\pm 5$

$x-3=5\ \text{or}\ x-3=-5$

Add 3 to both sides of each equation.

$x=5+3\ \text{or}\ x=-5+3$

$x=8\ \text{or}\ x=-2$

Report an Error

Example Question #3 : Exponents And The Distributive Property

Simplify:

$\left ( xyz \right )^{3}+x^{2}y+\left ( xy \right )^{0}+\left ( xy^{\frac{1}{2}} \right )^{2}$

Possible Answers:

$x^{3}y^{3}z^{3}+2x^{2}y$

$x^{3}y^{3}z^{3}+x^{2}y+1$

$x^{3}y^{3}z^{3}+2x^{2}y+1$

$x^{3}y^{3}z^{3}+x^{2}y$

$2x^{5}y^{3}z$

Correct answer:

$x^{3}y^{3}z^{3}+2x^{2}y+1$

Explanation:

$\left ( xyz \right )^{3}+x^{2}y+\left ( xy \right )^{0}+\left ( xy^{\frac{1}{2}} \right )^{2}$

= x³y³z³ + x²y + x⁰y⁰ + x²y

= x³y³z³ + x²y + 1 + x²y

= x³y³z³ + 2x²y + 1

Report an Error

Example Question #5 : Exponents And The Distributive Property

(6x^4+2x^2)(3x^4+6x^2)

Possible Answers:

42x^8

18x^8+42x^6+12x^4

18x^8+36x^6+12x^4

18x^8+12x^4

$18x^{16}+42x^8+12x^4$

Correct answer:

18x^8+42x^6+12x^4

Explanation:

Use the FOIL method to find the product. Remember to add the exponents when multiplying.

First: $6x^4\cdot3x^4 = 18x^8$

Outside: $6x^4\cdot6x^2=36x^6$

Inside: $2x^2\cdot 3x^4=6x^6$

Last: $2x^2\cdot6x^2=12x^4$

Add all the terms:

18x^8+36x^6+6x^6+12x^4

18x^8+42x^6+12x^4

Report an Error

Example Question #3 : Exponents And The Distributive Property

Square the binomial.

$(x^{2}y^{4}+xy^{6})^{2}$

Possible Answers:

$x^8y^8+x^2y^{12}$

$2x^{8}y^{20}$

$x^4y^8+2x^3y^{10}+x^2y^{12}$

$x^{4}y^{8}+x^{2}y^{12}$

$x^4y^{16}+2x^2y^{24}+xy^{36}$

Correct answer:

$x^4y^8+2x^3y^{10}+x^2y^{12}$

Explanation:

$(x^{2}y^{4}+xy^{6})^{2}$

$(x^{2}y^{4}+xy^{6})(x^{2}y^{4}+xy^{6})$

We will need to FOIL.

First: x^2y^4*x^2y^4=x^4y^8

Inside: $xy^6*x^2y^4=x^3y^{10}$

Outside: $x^2y^4*xy^6=x^3y^{10}$

Last: $xy^6*xy^6=x^2y^{12}$

Sum all of the terms and simplify.

$x^4y^8+x^3y^{10}+x^3y^{10}+x^2y^{12}$

$x^4y^8+2x^3y^{10}+x^2y^{12}$

Report an Error

View PSAT Mathematics Tutors

Tajrin
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Computer Science.

View PSAT Mathematics Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

View PSAT Mathematics Tutors

Germaine
Certified Tutor

Princeton University, Bachelor in Arts, Philosophy.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Dallas Fort Worth, GMAT Tutors in Chicago, GRE Tutors in Washington DC, Chemistry Tutors in Denver, ISEE Tutors in Boston, English Tutors in Atlanta, English Tutors in New York City, Physics Tutors in Boston, French Tutors in Denver, Statistics Tutors in Dallas Fort Worth

Popular Courses & Classes

SAT Courses & Classes in San Diego, MCAT Courses & Classes in New York City, SAT Courses & Classes in Denver, SAT Courses & Classes in Chicago, GMAT Courses & Classes in Washington DC, Spanish Courses & Classes in Washington DC, SAT Courses & Classes in Boston, SAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Washington DC, ACT Courses & Classes in Seattle

Popular Test Prep

ACT Test Prep in Washington DC, GMAT Test Prep in Phoenix, GMAT Test Prep in Seattle, ACT Test Prep in Philadelphia, GRE Test Prep in Miami, LSAT Test Prep in New York City, GMAT Test Prep in Los Angeles, SAT Test Prep in Chicago, GMAT Test Prep in Washington DC, GRE Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Exponents and the Distributive Property

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #1 : How To Use Foil

Example Question #1 : How To Use Foil

Example Question #1 : Exponents And The Distributive Property

Example Question #1 : Exponents And The Distributive Property

Example Question #5 : Exponents And The Distributive Property

Example Question #6 : Exponents And The Distributive Property

Example Question #2 : Exponents And The Distributive Property

Example Question #3 : Exponents And The Distributive Property

Example Question #5 : Exponents And The Distributive Property

Example Question #3 : Exponents And The Distributive Property

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: