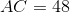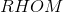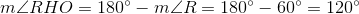The area of a rhombus is found by

A = 1/2(d₁)(d₂)

where d₁ and d₂ are the lengths of the diagonals.  Substituting for the given values yields

24 = 1/2(d₁)(6)

24 = 3(d₁)

8 = d₁

Now, use the facts that diagonals are perpendicular in a rhombus, diagonals bisect each other in a rhombus, and the Pythagorean Theorem to determine that the two diagonals form 4 right triangles with leg lengths of 3 and 4.  Since 3² + 4² = 5², each side length is 5, so the perimeter is 5(4) = 20.

\(\displaystyle AB=BC=CD=DA\), so Quadrilateral \(\displaystyle ABCD\) is a rhombus. Its diagonals are therefore perpendicular to each other, and the four triangles they form are right triangles. Therefore, the Pythagorean theorem can be used to determine the common sidelength of Quadrilateral \(\displaystyle ABCD\).

We focus on \(\displaystyle \Delta AXB\). The diagonals are also each other's bisector, so 

\(\displaystyle AX = \frac{1}{2} (AC) = \frac{1}{2} \cdot 48= 24\)

\(\displaystyle XB = \frac{1}{2} (BD) = \frac{1}{2} \cdot 20=10\)

By the Pythagorean Theorem, 

\(\displaystyle AB = \sqrt{(AX)^{2}+ (XB)^{2}} = \sqrt{24^{2}+10^{2}} = \sqrt{576+100} = \sqrt{676} = 26\)

26 is the common length of the four sides of Quadrilateral \(\displaystyle ABCD\), so its perimeter is \(\displaystyle 4 \times 26 = 104\).

The area of a rhombus will vary as the angles made by its sides change. The "flatter" the rhombus is (with two very small angles and two very large angles, say 2, 178, 2, and 178 degrees), the smaller the area is. There is, of course, a lower bound of zero for the area, but the area can get arbitrarily small. This implies that the correct answer would be the largest choice. In fact, the largest area of a rhombus occurs when all four angles are equal, i.e. when the rhombus is a square. The area of a square of side length 5 is 25, so any value bigger than 25 is impossible to acheive.

The figure referenced is below.

Consecutive angles of a rhombus are supplementary - as they are with all parallelograms - so

\(\displaystyle m \angle RHO= 180^{\circ} - m \angle R = 180^{\circ} - 60^{\circ} = 120^{\circ}\)

A diagonal of a rhombus bisects its angles, so 

\(\displaystyle m \angle RHM = \frac{1}{2} m \angle RHO= \frac{1}{2} \cdot 120^{\circ} = 60^{\circ}\)

A similar argument proves that \(\displaystyle m \angle RMH = 60^{\circ}\).

Since all three angles of \(\displaystyle \Delta RHM\) measure \(\displaystyle 60^{\circ}\), the triangle is acute. It is also equiangular, and, subsequently, equilateral.

The figure referenced is below.

The sides of a rhombus are congruent by definition, so \(\displaystyle \overline{RH} \cong \overline{HO}\), making \(\displaystyle \Delta RHO\) isosceles. It is not equilateral, since \(\displaystyle m \angle H = 45 ^{\circ }\), and an equilateral triangle must have three \(\displaystyle 60 ^{\circ}\) angles.

Also, consecutive angles of a rhombus are supplementary - as they are with all parallelograms - so

\(\displaystyle m \angle HRM = 180^{\circ} - m \angle H = 180^{\circ} - 45 ^{\circ} = 135^{\circ}\)

A diagonal of a rhombus bisects its angles, so 

\(\displaystyle m \angle HRO = \frac{1}{2} m \angle HRM = \frac{1}{2} \cdot 135 ^{\circ } = 67\frac{1}{2}^{\circ }\)

Similarly, \(\displaystyle m \angle HOR = 67\frac{1}{2}^{\circ }\)

This makes \(\displaystyle \Delta RHO\) acute.

The correct response is that \(\displaystyle \Delta RHO\) is acute and isosceles, but not equilateral.

Quadrilateral ABCD has four ninety-degree angles, which means that it has four right angles because every right angle measures ninety degrees. If a quadrilateral has four right angles, then it must be a rectangle by the definition of a rectangle. This means statement I is definitely true.

However, just because ABCD has four right angles doesn't mean that it is a rhombus. In order for a quadrilateral to be considered a rhombus, it must have four congruent sides. It's possible to have a rectangle whose sides are not all congruent. For example, if a rectangle has a width of 4 meters and a length of 8 meters, then not all of the sides of the rectangle would be congruent. In fact, in a rectangle, only opposite sides need be congruent. This means that ABCD is not necessarily a rhombus, and statement II does not have to be true.

A square is defined as a rhombus with four right angles. In a square, all of the sides must be congruent. In other words, a square is both a rectangle and a rhombus. However, we already established that ABCD doesn't have to be a rhombus. This means that ABCD need not be a square, because, as we said previously, not all of its sides must be congruent. Therefore, statement III isn't necessarily true either.

The only statement that has to be true is statement I.

The answer is I only.

In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:

area of trapezoid = (1/2)(4 + s)(s)

Similarly, the area of a square with sides of length a is given by a². Thus, the area of the square given in the problem is s².

We now can set the area of the trapezoid equal to the area of the square and solve for s.

(1/2)(4 + s)(s) = s²

Multiply both sides by 2 to eliminate the 1/2.

(4 + s)(s) = 2s²

Distribute the s on the left.

4s + s² = 2s²

Subtract s² from both sides.

4s = s²

Because s must be a positive number, we can divide both sides by s.

4 = s

This means the value of s must be 4.

The answer is 4.

The area of the entire rectangle is the product of its length and width, or

\(\displaystyle 100 \times 50 = 5,000\).

The area of the white trapezoid is one half the product of its height and the sum of its base lengths, or 

\(\displaystyle \frac{1}{2} \times (64+100) \times 18 = 1,476\)

Therefore, the blue polygon has area 

\(\displaystyle 5,000 - 1,476= 3,524\). 

This is 

\(\displaystyle \frac{3,524}{5,000} \times 100 = 70.48 \%\) of the rectangle.

Rounded, this is 70%.

 \(\displaystyle \angle C \cong \angle BDX\), since both are right; by the Corresponding Angles Theorem,  \(\displaystyle \overline{AC} || \overline{BD}\), and Quadrilateral \(\displaystyle ABDC\) is a trapezoid.

By the Angle-Angle Similarity Postulate, since 

\(\displaystyle \angle C \cong \angle BDX\) 

and

\(\displaystyle \angle X \cong \angle X\) (by reflexivity),

\(\displaystyle \Delta ACX \sim \Delta BDX\), 

and since corresponding sides of similar triangles are in proportion,

\(\displaystyle \frac{AC}{CX} = \frac{BD}{DX}\)

\(\displaystyle \frac{AC}{24} = \frac{6}{9}\)

\(\displaystyle \frac{AC}{24} \times 24 = \frac{6}{9} \times 24\)

\(\displaystyle AC = 16\), the larger base of the trapozoid;

The smaller base is \(\displaystyle BD = 6\).

\(\displaystyle CD = CX - DX = 24-9 = 15\), the height of the trapezoid.

The area of the trapezoid is 

\(\displaystyle A = \frac{1}{2} (b + B)h\)

\(\displaystyle A = \frac{1}{2} (BD + AC) \cdot CD\)

\(\displaystyle A = \frac{1}{2} (6+ 16) \cdot 15 = \frac{1}{2} (22) \cdot 15 = 165\)

To inscribe means to draw inside a figure so as to touch in as many places as possible without overlapping. The circle is inside the square such that the diameter of the circle is the same as the side of the square, so the side is actually 4 in.  The perimeter of the square = 4s = 4 * 4 = 16 in.