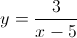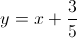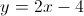Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Solving Functions

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Solving Linear Functions

Solve for in terms of .

3y-xy+7=2

Possible Answers:

$y=\frac{5}{x+3}$

$y=x+\frac{3}{5}$

$y=\frac{3}{x-5}$

$y=\frac{5}{x-3}$

$y=\frac{-5}{x-3}$

Correct answer:

$y=\frac{5}{x-3}$

Explanation:

First, subtract 7 to both sides.

3y-xy+7=2

3y-xy=-5

Factor the y on the left hand side.

y(3-x)=-5

Divide both sides by 3 – x.

$y=\frac{-5}{3-x}$

Take an extra step by factoring the minus sign on the denominator.

$y=\frac{-5}{-(x-3)}$

Cancel the minus signs.

$y=\frac{5}{x-3}$

Report an Error

Example Question #26 : How To Find The Equation Of A Line

Find the equation for the line goes through the two points below.

(1,-2)

(-3, 6)

Possible Answers:

$y = \frac{1}{2}x + 4$

y = -2x

$y = \frac{1}{2}x$

y = 4x - 2

y = 2x -4

Correct answer:

y = -2x

Explanation:

Let $P_{1} = (1, \; -2) \; \; and \; \; P_{2} = (-3, \; 6)$ .

First, calculate the slope between the two points.

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{6 - (-2)}{-3 - 1} = \frac{8}{-4} = -2$

Next, use the slope-intercept form to calculate the intercept. We are able to plug in our value for the slope, as well the the values for P_1 .

y = mx + b

-2 = -2(1) + b

b=0

Using slope-intercept form, where we know m=-2 and b=0 , we can see that the equation for this line is y = -2x .

Report an Error

Example Question #3 : Solving Linear Functions

Find the equation of the line passing through the points $\small (-3,2)$ and $\small (1,8)$ .

Possible Answers:

$\small y=-\frac{3}{2}x+\frac{13}{2}$

$\small y=-\frac{2}{3}x+\frac{13}{2}$

$\small y=\frac{2}{3}x-\frac{13}{2}$

$\small y=\frac{2}{3}x+\frac{13}{2}$

$\small y=\frac{3}{2}x+\frac{13}{2}$

Correct answer:

$\small y=\frac{3}{2}x+\frac{13}{2}$

Explanation:

To calculate a line passing through two points, we first need to calculate the slope, $\small m$ .

$\small m=\frac{\Delta y}{\Delta x} =\frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{8-2}{1-(-3)} = \frac{6}{4} = \frac{3}{2}$

Now that we have the slope, we can plug it into our equation for a line in slope intercept form.

$\small y=\frac{3}{2}x+b$

To solve for $\small b$ , we can plug in one of the points we were given. For the sake of this example, let's use $\small (-3,2)$ , but realize either point will give use the same answer.

$\small 2=\frac{3}{2}(-3)+b$

$\small 2=\frac{-9}{2}+b$

$\small 2+\frac{9}{2} = b$

$\small \frac{13}{2} = b$

Now that we have solved for b, we can plug that into our slope intercept form and produce and the answer

$\small y=\frac{3}{2}x+\frac{13}{2}$

Report an Error

Example Question #1 : Solving Linear Functions

Find the point at which these two lines intersect:

$\small 2x+5y=8$

$\small \small \small -2x+2y=-1$

Possible Answers:

$\left(\frac{3}{2},1\right)$

$\left(-\frac{3}{2},1\right)$

$\left(1,\frac{3}{2}\right)$

$\left(1,-\frac{3}{2}\right)$

Correct answer:

$\left(\frac{3}{2},1\right)$

Explanation:

We are looking for a point, $\small (x,y)$ , where these two lines intersect. While there are many ways to solve for $\small x$ and $\small y$ given two equations, the simplest way I see is to use the elimination method since by adding the two equations together, we can eliminate the $\small x$ variable.

7y=7

Dividing both sides by 7, we isolate y.

$\small y=1$

Now, we can plug y back into either equation and solve for x.

$\small 2x+(5)(1)=8$

$\small 2x+5=8$

Next, we can solve for x.

$\small 2x=3$

$\small x=(3/2)$

Therefore, the point where these two lines intersect is $\left(\frac{3}{2}, 1\right)$ .

Report an Error

Example Question #1 : Solving Linear Functions

$y=\frac{1}{3}x+9$

Solve for when y=2 .

Possible Answers:

Correct answer:

Explanation:

The first thing is to plug in the given value so you equation is

$2=\frac{1}{3}x+9$ .

Then you must subtract from both sides in order to get by itself.

You now have

$-7=\frac{1}{3}x$

and you must multiply by for each side and you get x=-21 .

Report an Error

Example Question #2 : Solving Linear Functions

Solve: -7x-16 = 3x+2

Possible Answers:

$-\frac{9}{5}$

$-\frac{9}{2}$

$\frac{3}{4}$

$-\frac{7}{2}$

Correct answer:

$-\frac{9}{5}$

Explanation:

Add on both sides.

-7x-16 +(7x)= 3x+2+(7x)

-16 = 10x+2

Subtract 2 from both sides.

-16 -2= 10x+2-2

-18 = 10x

Divide by 10 on both sides.

$\frac{-18}{10} =\frac{ 10x}{10}$

Reduce the fractions.

The answer is: $-\frac{9}{5}$

Report an Error

Example Question #7 : Solving Linear Functions

Solve: 3x+5 = -2(2-3x)

Possible Answers:

$\frac{1}{3}$

$\frac{7}{3}$

$\frac{4}{3}$

Correct answer:

Explanation:

Distribute the right side.

-2(2-3x) = -4 +6x

Rewrite the equation.

3x+5 = -4+6x

Subtract on both sides.

3x+5 -3x= -4+6x-3x

5=-4+3x

Add 4 on both sides.

5+4=-4+3x+4

9=3x

Divide by three on both sides.

$\frac{9}{3}=\frac{3x}{3}$

The answer is:

Report an Error

Example Question #1 : Solving Exponential Functions

Solve the following function:

$11=x^{2}-5$

Possible Answers:

and

Correct answer:

and

Explanation:

You must get by itself so you must add to both side which results in

$16=x^{2}$ .

You must get the square root of both side to undue the exponent.

This leaves you with x=4 .

But since you square the in the equation, the original value you plug can also be its negative value since squaring it will make it positive anyway.

This means your answer can be x=4 or x=-4 .

Report an Error

Example Question #1 : Solving Exponential Functions

What is the horizontal asymptote of the graph of the equation $y = -2e^{x-3} -5$ ?

Possible Answers:

y=-2

y=5

$y=-\frac{5}{2}$

y=-5

y=3

Correct answer:

y=-5

Explanation:

The asymptote of this equation can be found by observing that $e^{x-3} > 0$ regardless of . We are thus solving for the value of as $e^{x-3}$ approaches zero.

$-2e^{x-3} < -2\cdot 0$

$-2e^{x-3} < 0$

$-2e^{x-3} -5 < 0-5$

$-2e^{x-3} -5 < -5$

y<-5

So the value that cannot exceed is , and the line y = -5 is the asymptote.

Report an Error

Example Question #1 : Solving Exponential Functions

What is/are the asymptote(s) of the graph of the function

$f(x) = 5e^{x-2}-2$ ?

Possible Answers:

x=2

y = -2

y = -2, x=-2

y = -2, x=2

x=-2

Correct answer:

y = -2

Explanation:

An exponential equation of the form $f(x) = ae^{x-h} +k$ has only one asymptote - a horizontal one at y = k . In the given function, k = -2 , so its one and only asymptote is y = -2 .

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Subject Test in Mathematics Level 1 Tutors

Samarth
Certified Tutor

Maharaja Sayajirao University of Baroda, Bachelor of Engineering, Mechanical Engineering. Concordia University-Seward, Master...

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Houston, SAT Tutors in Miami, Spanish Tutors in San Francisco-Bay Area, Calculus Tutors in San Diego, MCAT Tutors in Miami, English Tutors in Phoenix, Statistics Tutors in Atlanta, ACT Tutors in Philadelphia, Algebra Tutors in New York City, Biology Tutors in New York City

Popular Courses & Classes

GMAT Courses & Classes in Boston, MCAT Courses & Classes in Los Angeles, SSAT Courses & Classes in Chicago, ACT Courses & Classes in Houston, LSAT Courses & Classes in Houston, SSAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Philadelphia, GMAT Courses & Classes in Phoenix, LSAT Courses & Classes in New York City, ISEE Courses & Classes in Chicago

Popular Test Prep

MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Houston, GMAT Test Prep in Phoenix, ISEE Test Prep in San Francisco-Bay Area, LSAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Houston, GMAT Test Prep in Atlanta, SAT Test Prep in Philadelphia, SSAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Solving Functions

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #1 : Solving Linear Functions

Example Question #26 : How To Find The Equation Of A Line

Example Question #3 : Solving Linear Functions

Example Question #1 : Solving Linear Functions

Example Question #1 : Solving Linear Functions

Example Question #2 : Solving Linear Functions

Example Question #7 : Solving Linear Functions

Example Question #1 : Solving Exponential Functions

Example Question #1 : Solving Exponential Functions

Example Question #1 : Solving Exponential Functions

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: