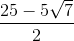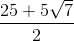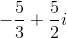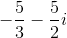All SAT II Math I Resources
Example Questions
Example Question #1 : Irrational Numbers
Which of the following is not an irrational number?
A root of an integer is one of two things, an integer or an irrational number. By testing all five on a calculator, only ![\sqrt[3]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214986/gif.latex)
Example Question #1 : Irrational Numbers
Simplify by rationalizing the denominator:
Multiply the numerator and the denominator by the conjugate of the denominator, which is 
Example Question #7 : Number Theory
Example Question #8 : Number Theory
Multiply:
Use the FOIL technique:
Example Question #1 : Irrational Numbers
Evaluate:
We can set 
Example Question #2 : Irrational Numbers
Evaluate
You cannot divide by complex numbers
To divide by a complex number, we must transform the expression by multiplying it by the complex conjugate of the denominator over itself. In the problem, 


We can then combine like terms and rewrite all 

Our final answer is therefore
Example Question #1 : Irrational Numbers
Simplify the following product:
Multiply these complex numbers out in the typical way:
and recall that 
which is our final answer.
Example Question #2 : Irrational Numbers
Identify the real part of
none of the above.
A complex number in its standard form is of the form: 




The real part in this problem is 1.
Example Question #1 : Complex Imaginary Numbers
Simplify:
To add complex numbers, find the sum of the real terms, then find the sum of the imaginary terms.
Example Question #1 : Irrational Numbers
Simplify:
Start by using FOIL. Which means to multiply the first terms together then the outer terms followed by the inner terms and lastly, the last terms.
Remember that 

Substitute in 
All SAT II Math I Resources

![\sqrt[6]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214962/gif.latex)
![\sqrt[5]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214961/gif.latex)
![\sqrt[2]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214959/gif.latex)
![\sqrt[4]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214960/gif.latex)
![\sqrt[3]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214958/gif.latex)