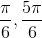All SAT II Math I Resources
Example Questions
Example Question #621 : Sat Subject Test In Math I
Solve for 
![[0,2\pi]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/235309/gif.latex)
First we must solve for when sin is equal to 1/2. That is at
Now, plug it in:
Example Question #622 : Sat Subject Test In Math I
Solve for 
![[0,2\pi]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/235309/gif.latex)
First we must solve for when sin is equal to 1/2. That is at
Now, plug it in:
Example Question #2 : Trigonometry
In a triangle, 

(Round answer to the nearest tenth of a degree.)
To find the measure of angle of A we will use tangent to solve for A. We know that
In our case opposite = 3 and adjacent = 4, we substitute these values in and get:
Now we take the inverse tangent of each side to find the degree value of A.
Example Question #1 : Trigonometry
If 




Recall that 
Therefore, we are looking for 

Now, this has a reference angle of 



Example Question #11 : Trigonometry
Determine the exact value of 
The exact value of 
The x-value of this angle is 
Example Question #11 : Trigonometry

Which of the following is equal to cos(x)?
Remember SOH-CAH-TOA! That means:





sin(y) is equal to cos(x)
Example Question #1 : Sin, Cos, Tan
Find the value of 
To find the value of 
Sum the two terms.
Example Question #1 : Sin, Cos, Tan
Calculate 
The tangent function has a period of 
for all 
Since 

Hence,
Example Question #3 : Sin, Cos, Tan
Calculate 
First, convert the given angle measure from radians to degrees:
Next, recall that 

Hence, all that is required is to recognize from these observations that

which is 
Therefore,
Certified Tutor
Certified Tutor
All SAT II Math I Resources