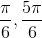Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Trigonometry

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Trigonometry

A plane flies degrees north of east for 100 miles. It then turns and flies degrees south of east for 200 miles. Approximately how many miles is the plane from its starting point? (Ignore the curvature of the Earth.)

Possible Answers:

297

205

139

121

172

Correct answer:

139

Explanation:

The plane flies two sides of a triangle. The angle formed between the two sides is 40 degrees. In a Side-Angle-Side situation, it is appropriate to employ the use of the Law of Cosines.

$c^2 = a^2 + b^2 - 2ab \cos C$

$c^2 = 100^2 + 200^2 - 2(100)(200) \cos 40^{\circ}$

$c^2 \approx 19358$

$c \approx \sqrt{19358} \approx 139$

Report an Error

Example Question #1 : Trigonometry

In $\bigtriangleup ABC$ :

AB = 13

AC = 17

BC = 25

Evaluate $m \angle A$ to the nearest degree.

Possible Answers:

Insufficient information is provided to answer the question.

$151^{\circ }$

$68^{\circ }$

$112 ^{\circ }$

$141^{\circ }$

Correct answer:

$112 ^{\circ }$

Explanation:

The figure referenced is below:

Triangle z

By the Law of Cosines, the relationship of the measure of an angle $\gamma$ of a triangle and the three side lengths , , and , the sidelength opposite the aforementioned angle, is as follows:

$c^{2} = a ^{2} + b^{2} - 2ab \cos \gamma$

All three sidelengths are known, so we are solving for $\gamma$ . Setting

c= BC = 25 . the length of the side opposite the unknown angle;

a = AB = 13 ;

b = AC = 17 ;

and $\gamma = \cos A$ ,

We get the equation

$25^{2} =13^{2} +17^{2} - 2 (13) (17)\cos A$

$625 =169 +289- 442 \cos A$

$625 =458- 442 \cos A$

Solving for $\cos A$ :

$625 - 458 =458- 442 \cos A - 458$

$167 = - 442 \cos A$

$\frac{167}{-442} = \frac{- 442 \cos A}{-442}$

$\cos A \approx -0.3778$

Taking the inverse cosine:

$A = \cos ^{-1} -0.3778 \approx 112 ^{\circ }$ ,

the correct response.

Report an Error

Example Question #1 : Finding Sides With Trigonometry

In $\bigtriangleup ABC$ :

AB = 19

AC = 25

$m \angle A = 57^{\circ }$

Evaluate the length of $\overline{BC}$ to the nearest tenth of a unit.

Possible Answers:

38.8

13.7

27.0

24.2

21.6

Correct answer:

21.6

Explanation:

The figure referenced is below:

Triangle z

By the Law of Cosines, given the lengths and of two sides of a triangle, and the measure $\gamma$ of their included angle, the length of the third side can be calculated using the formula

$c^{2} = a ^{2} + b^{2} - 2ab \cos \gamma$

Substituting a = AB = 19 , b = AC = 25 , c = BC , and $\gamma = m \angle A = 57^{\circ }$ , then evaluating:

$(BC)^{2} = 19 ^{2} + 25 ^{2} - 2 (19)(25)\cos 57^{\circ }$

$(BC)^{2} \approx 361 + 625 - 950 \cdot 0.5446$

$(BC)^{2} \approx 361 + 625 - 517.4$

$(BC)^{2} \approx 468.6$

Taking the square root of both sides:

$BC \approx \sqrt{468.6} \approx 21.6$ .

Report an Error

Example Question #3 : Finding Sides With Trigonometry

In $\bigtriangleup ABC$ :

$m \angle A = 76 ^{\circ }$

$m \angle B = 65 ^{\circ }$

AB = 34

$\textup{Evaluate}$ $\textup{to the nearest whole unit.}$

Possible Answers:

Correct answer:

Explanation:

The figure referenced is below:

Triangle z

The Law of Sines states that given two angles of a triangle with measures $\alpha, \beta$ , and their opposite sides of lengths a,b , respectively,

$\frac{\sin \beta}{b} = \frac{\sin \gamma}{c}$ ,

or, equivalently,

$\frac{b}{\sin \beta} = \frac{c}{\sin \gamma}$ .

In this formula, we set:

b = AC , the desired sidelength;

$\beta =m \angle B = 65^{\circ }$ , the measure of its opposite angle;

c =AB = 34 , the known sidelength;

$\gamma =m \angle C$ , the measure of its opposite angle, which is

$m \angle C = 180 ^{\circ } - (m \angle A + m \angle B)$

$= 180 ^{\circ } - ( 76^{\circ } + 65 ^{\circ })$

$= 180 ^{\circ } - 141 ^{\circ }$

$=39 ^{\circ }$

Substituting in the Law of Sines formula and solving for :

$\frac{b}{\sin \beta} = \frac{c}{\sin \gamma}$

$\frac{b}{\sin 65 ^{\circ }} = \frac{ 34}{\sin 39 ^{\circ }}$

$\frac{b}{\sin 65 ^{\circ }} \cdot \sin 65 ^{\circ } = \frac{ 34}{\sin 39 ^{\circ }} \cdot \sin 65 ^{\circ }$

$b= \frac{ 34}{\sin 39 ^{\circ }} \cdot \sin 65 ^{\circ }$

Evaluating the sines, then calculating:

$b\approx \frac{ 34}{0.6293 } \cdot 0.9063$

$b \approx 49$

Report an Error

Example Question #1 : Finding Angles With Trigonometry

What is the measure of the angle made between a line segment with points (0,0) , (5,8) and the -axis? Round your answer to the nearest hundreth of a degree.

Possible Answers:

$12.42^{\circ}$

$82.87^{\circ}$

No angle measure can be calculated

$71.42{^{\circ}}$

$58.00^{\circ}$

Correct answer:

$58.00^{\circ}$

Explanation:

Based on the information given, we know that the ratio of to on this segment could be represented as:

$\frac{8}{5}$

This ratio represents the tangent of the triangle formed by our line segment and the -axis. Using the inverse tangent function, we can find the angle measure:

$\tan^{-1}(\frac{8}{5}) = 57.9946167919165$

This refers to a reference angle of $58.00^{\circ}$

Report an Error

Example Question #1 : Trigonometry

What is the measure of the angle made between a line segment with points (0,0) , (-8,7) and the -axis? Round your answer to the nearest hundreth of a degree.

Possible Answers:

$48.81^{\circ}$

$-48.81^{\circ}$

$71.41^{\circ}$

No angle can be calculated

$41.10^{\circ}$

Correct answer:

$48.81^{\circ}$

Explanation:

Based on the information given, we know that the ratio of to on this segment could be represented as:

$\frac{-8}{7}$

This ratio represents the tangent of the triangle formed by our line segment and the -axis. Using the inverse tangent function, we can find the angle measure:

$\tan^{-1}(\frac{-8}{7}) = -48.81407483429027$

This refers to a reference angle of $48.81^{\circ}$ .

Report an Error

Example Question #1 : Trigonometry

A triangle is formed by connecting the points $(0,0), (1,0), \textup{ and }(1,6)$ . Determine the elevation angle to the nearest integer in degrees.

Possible Answers:

Correct answer:

Explanation:

After connecting the points on the graph, the length of the triangular base is 1 unit.

The height of the triangle is 6. To find the elevation angle, the angle is opposite from the height of the triangle. Since we know the base and the height, the elevation angle can be solved by using the property of tangent.

$tan(\theta)= \frac{\textup{Opposite side}}{\textup{Adjacent side}}$

$tan(\theta)= \frac{\textup{6}}{\textup{1}}$

$\theta = tan^{-1}(6)=80.53768 \textup{ degrees}$

The best answer is .

Report an Error

Example Question #1 : Sine, Cosine, Tangent

Solve for $\theta$ between $[0,2\pi]$ .

$\sin (2\theta )=\frac{1}{2}$

Possible Answers:

$\frac{\pi}{6},\frac{\pi}{3}$

$\frac{\pi}{3},\frac{2\pi}{3}$

$\frac{\pi}{12},\frac{5\pi}{12}$

$\frac{\pi}{6},\frac{5\pi}{6}$

Correct answer:

$\frac{\pi}{12},\frac{5\pi}{12}$

Explanation:

First we must solve for when sin is equal to 1/2. That is at

$\frac{\pi}{6},\frac{5\pi}{6}$

Now, plug it in:

$2\theta =\frac{\pi}{6}\Rightarrow \theta =\frac{\pi}{12}$

$2\theta =\frac{5\pi}{6}\Rightarrow \theta =\frac{5\pi}{12}$

Report an Error

Example Question #2 : Trigonometry

Solve for $\theta$ between $[0,2\pi]$ .

$\cos (2\theta )=\frac{1}{2}$

Possible Answers:

$\frac{\pi}{3},\frac{5\pi}{3}$

$\frac{\pi}{3},\frac{2\pi}{3}$

$\frac{\pi}{6},\frac{5\pi}{6}$

$\frac{\pi}{12},\frac{5\pi}{12}$

Correct answer:

$\frac{\pi}{6},\frac{5\pi}{6}$

Explanation:

First we must solve for when sin is equal to 1/2. That is at

$\frac{\pi}{3},\frac{5\pi}{3}$

Now, plug it in:

$2\theta =\frac{\pi}{3}\Rightarrow \theta =\frac{\pi}{6}\,$

$2\theta =\frac{5\pi}{3}\Rightarrow \theta =\frac{5\pi}{6}$

Report an Error

Example Question #2 : Trigonometry

In a triangle, ABC , what is the measure of angle A if the side opposite of $\angleA$ angle A is 3 and the adjacent side to angle A is 4?

(Round answer to the nearest tenth of a degree.)

Possible Answers:

$36.9^{\circ}$

$34.7^{\circ}$

$32^{\circ}$

$40^{\circ}$

Correct answer:

$36.9^{\circ}$

Explanation:

To find the measure of angle of A we will use tangent to solve for A. We know that

$tan A=\frac{opposite}{adjacent}$

In our case opposite = 3 and adjacent = 4, we substitute these values in and get:

$tan A= \frac{3}{4}$

Now we take the inverse tangent of each side to find the degree value of A.

$A= tan^{^{-1}}\left(\frac{3}{4}\right)$

A=36.9

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Subject Test in Mathematics Level 1 Tutors

Samarth
Certified Tutor

Maharaja Sayajirao University of Baroda, Bachelor of Engineering, Mechanical Engineering. Concordia University-Seward, Master...

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in New York City, Math Tutors in Boston, Reading Tutors in Denver, Math Tutors in Houston, Spanish Tutors in Phoenix, Biology Tutors in Los Angeles, Chemistry Tutors in Boston, English Tutors in San Diego, Spanish Tutors in New York City, Computer Science Tutors in Phoenix

Popular Courses & Classes

GRE Courses & Classes in Atlanta, SSAT Courses & Classes in Philadelphia, SAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Chicago, LSAT Courses & Classes in Los Angeles, SSAT Courses & Classes in Miami, SSAT Courses & Classes in Denver, GMAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Chicago, SSAT Courses & Classes in Los Angeles

Popular Test Prep

GRE Test Prep in Miami, ACT Test Prep in Denver, LSAT Test Prep in Los Angeles, LSAT Test Prep in Seattle, SSAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Los Angeles, GMAT Test Prep in Boston, LSAT Test Prep in Philadelphia, ISEE Test Prep in Chicago, GMAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Trigonometry

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #1 : Trigonometry

Example Question #1 : Trigonometry

Example Question #1 : Finding Sides With Trigonometry

Example Question #3 : Finding Sides With Trigonometry

Example Question #1 : Finding Angles With Trigonometry

Example Question #1 : Trigonometry

Example Question #1 : Trigonometry

Example Question #1 : Sine, Cosine, Tangent

Example Question #2 : Trigonometry

Example Question #2 : Trigonometry

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: