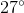A regular pentagon can be divided into ten congruent triangles by its five radii and its five apothems. Each triangle has the following shape:

The area of one such triangle is $\displaystyle \frac{1}{2}ab$, so the area of the entire pentagon is ten times this, or $\displaystyle 10 \cdot \frac{1}{2}ab = 5ab$.

The area of the pentagon is 1,000, so

$\displaystyle 5ab = 1,000$

$\displaystyle ab = 200$

Also,

$\displaystyle \frac{a}{b} = \tan 54^{\circ }$, or equivalently, $\displaystyle a=b \tan 54^{\circ }$, so we solve for $\displaystyle b$ in the equation:

$\displaystyle b \tan 54^{ \circ } \cdot b = 200$

$\displaystyle b^{2} \tan 54^{ \circ } = 200$

$\displaystyle b^{2} = \frac{200}{\tan 54^{ \circ }} \approx \frac{200}{ 1.3764} \approx 145.3$

$\displaystyle b \approx \sqrt{145.3} \approx 12.1$

The perimeter is ten times this, or 121.

A regular dodecagon can be divided into twenty-four congruent triangles by its twelve radii and its twelve apothems, each of which is shaped as shown:

The area of one such triangle is $\displaystyle \frac{1}{2}ab$, so the area of the entire dodecagon is twenty-four times this, or 

$\displaystyle 24 \cdot \frac{1}{2}ab = 12ab$.

The area of the dodecagon is 600, so

$\displaystyle 12ab = 600$, or

$\displaystyle ab = 50$.

Also,

$\displaystyle \frac{a}{b} = \tan 75^{\circ }$, or equivalently, $\displaystyle a=b \tan 75^{\circ }$, so solve for $\displaystyle b$ in the equation

$\displaystyle b \tan 75^{ \circ } \cdot b =50$

Solve for $\displaystyle b$:

$\displaystyle b^{2} \cdot \tan 75^{ \circ } = 50$

$\displaystyle b^{2} = \frac{50}{ \tan 75^{ \circ }} \approx \frac{50}{ 3.7321} \approx 13.4$

$\displaystyle b \approx \sqrt{13.4} \approx 3.66$

The perimeter is twenty-four times this:

$\displaystyle P \approx 3.66 \cdot 24 \approx 88$

A regular nonagon can be divided into eighteen congruent triangles by its nine radii and its nine apothems, each of which is shaped as shown:

The area of one such triangle is $\displaystyle \frac{1}{2}ab$, so the area of the entire nonagon is eighteen times this, or $\displaystyle 18 \cdot \frac{1}{2}ab = 9ab$. Since the area is 900,

$\displaystyle 9ab = 900$, or

$\displaystyle ab= 100$.

Also,

$\displaystyle \frac{a}{b} = \tan 70^{\circ }$, or equivalently, $\displaystyle a=b \tan 70^{\circ }$, so solve for $\displaystyle b$ in the equation

$\displaystyle b \tan 70^{\circ } \cdot b= 100$

$\displaystyle b ^{2} \cdot \tan 70^{\circ } = 100$

$\displaystyle b ^{2} = \frac{100}{\tan 70^{\circ } } \approx \frac{100}{ 2.7475 } \approx 36.40$

$\displaystyle b \approx \sqrt{36.40} \approx 6.03$

The perimeter of the nonagon is eighteen times this:

$\displaystyle 18 \cdot 6.03 \approx 109$, the correct response.

Construct the nonagon with diagonal $\displaystyle \overline{AC}$.

We will concern ourselves with finding the length of $\displaystyle \overline{BC}$.

Since $\displaystyle m \angle ABC = \frac{(9-2)\cdot 180^{ \circ}}{9}= 140 ^{ \circ}$, and $\displaystyle \Delta ABC$ is isosceles, then  

$\displaystyle m \angle BAC = \frac{1}{2} (180^{\circ } - 140^{\circ }) = 20^{\circ }$

The following diagram is formed (limiiting ourselves to $\displaystyle \Delta ABC$):

By the Law of Sines,

$\displaystyle \frac{BC}{\sin \left (m \angle BAC \right )} = \frac{AC} {\sin \left (m \angle ABC \right )}$

$\displaystyle \frac{BC}{\sin 20^{\circ }} = \frac{10} {\sin 140^{\circ }}$

$\displaystyle BC= \frac{10\sin 20^{\circ }} {\sin 140^{\circ }}$

$\displaystyle BC\approx \frac{10\cdot 0.3420} {0.6428}$

$\displaystyle BC \approx 5.3$

Construct the pentagon with diagonal $\displaystyle \overline{AC}$.

We will concern ourselves with finding the length of $\displaystyle \overline{BC}$.

Since $\displaystyle m \angle ABC = \frac{(5-2)\cdot 180^{ \circ}}{5}= 108 ^{ \circ}$, and $\displaystyle \Delta ABC$ is isosceles, then  

$\displaystyle m \angle BAC = \frac{1}{2} (180^{\circ } - 108^{\circ }) = 36^{\circ }$

The following diagram is formed:

By the Law of Sines,

$\displaystyle \frac{BC}{\sin \left (m \angle BAC \right )} = \frac{AC} {\sin \left (m \angle ABC \right )}$

$\displaystyle \frac{BC}{\sin 36^{\circ }} = \frac{10} {\sin 108^{\circ }}$

$\displaystyle BC= \frac{10\sin 36^{\circ }} {\sin 108^{\circ }}$

$\displaystyle BC\approx \frac{10\cdot 0.5878} {0.9511}$

$\displaystyle BC \approx 6.2$

The Law of Sines states that given two angles of a triangle with measures $\displaystyle \alpha, \beta$, and their opposite sides of lengths $\displaystyle a,b$, respectively,

$\displaystyle \frac{\sin \alpha}{a} = \frac{\sin \beta}{b}$,

or, equivalently,

$\displaystyle \frac{b}{\sin \beta} = \frac{a}{\sin \alpha}$.

$\displaystyle \overline{AC }$, whose length is desired, and $\displaystyle \overline{BC}$, whose length is given, are opposite $\displaystyle \angle B$ and $\displaystyle \angle A$, respectively, so, in the sine formula, set $\displaystyle b = AC$, $\displaystyle \beta = m \angle B = 20 ^{\circ }$, $\displaystyle a = BC = 40$, and $\displaystyle \alpha = m \angle A = 116^{\circ }$ in the Law of Sines formula, then solve for $\displaystyle AC$:

$\displaystyle \frac{AC}{\sin 20^{\circ }} = \frac{40}{\sin 116^{\circ }}$

$\displaystyle \frac{AC}{\sin 20^{\circ }} \cdot \sin 20^{\circ } = \frac{40}{\sin 116^{\circ }} \cdot \sin 20^{\circ }$

$\displaystyle AC = \frac{40}{\sin 116^{\circ }} \cdot \sin 20^{\circ }$

$\displaystyle \approx \frac{40}{0.8988} \cdot 0.3420$

$\displaystyle \approx 15$

The height of the tree requires using trigonometry to solve.  The distance of the student to the tree $\displaystyle (20)$, partial height of the tree $\displaystyle (P)$, and the distance between the student's eyes to the top of the tree will form the right triangle.

The tangent operation will be best used for this scenario, since we have the known distance of the student to the tree, and the partial height of the tree.

Set up an equation to solve for the partial height of the tree.

$\displaystyle tan(\theta) = \frac{\textup{Opposite side to angle}}{\textup{Adjacent side to angle}}$

$\displaystyle tan(30) = \frac{P}{20}$

Multiply by 20 on both sides.

$\displaystyle P=20tan(30) = 20(\frac{\sqrt{3}}{3}) = \frac{20\sqrt{3}}{3}$

We will need to add this with the height of the student's eyes to the ground to get the height of the tree.

$\displaystyle \frac{20\sqrt{3}}{3} + 4 = \frac{20\sqrt{3}}{3} + \frac{12}{3}$

The answer is:  $\displaystyle \frac{20\sqrt{3}+12}{3}$

Construct the decagon with diagonal $\displaystyle \overline{AC}$.

We will concern ourselves with finding the length of $\displaystyle \overline{BC}$.

Since $\displaystyle m \angle ABC = \frac{(10-2)\cdot 180^{ \circ}}{10}= 144 ^{ \circ}$, and $\displaystyle \Delta ABC$ is isosceles, then  

$\displaystyle m \angle BAC = \frac{1}{2} (180^{\circ } - 144^{\circ }) = 18^{\circ }$

The following diagram is formed (limiting ourselves to $\displaystyle \Delta ABC$):

By the Law of Sines,

$\displaystyle \frac{BC}{\sin \left (m \angle BAC \right )} = \frac{AC} {\sin \left (m \angle ABC \right )}$

$\displaystyle \frac{BC}{\sin 18^{\circ }} = \frac{10} {\sin 144^{\circ }}$

$\displaystyle BC= \frac{10\sin 18^{\circ }} {\sin 144^{\circ }}$

$\displaystyle BC\approx \frac{10\cdot 0.3090} {0.5878}$

$\displaystyle BC \approx 5.3$

The figure referenced is below: 

By the Law of Cosines, the relationship of the measure of an angle $\displaystyle \gamma$ of a triangle and the three side lengths $\displaystyle a$, $\displaystyle b$, and $\displaystyle c$, $\displaystyle c$ the sidelength opposite the aforementioned angle, is as follows:

$\displaystyle c^{2} = a ^{2} + b^{2} - 2ab \cos \gamma$

All three side lengths are known, so we are solving for $\displaystyle \gamma$. Setting

$\displaystyle c = BC = 25$, the length of the side opposite the unknown angle;

$\displaystyle a = AB = 23$;

$\displaystyle b = AC = 34$;

and $\displaystyle \gamma = \cos A$,

We get the equation

$\displaystyle 25^{2} =23^{2} +34^{2} - 2 (23) (34)\cos A$

$\displaystyle 625 =529+1,156- 1,564 \cos A$

$\displaystyle 625 =1,685 - 1,564 \cos A$

Solving for $\displaystyle \cos A$:

$\displaystyle 625 - 1,685 =1,685 - 1,564 \cos A - 1,685$

$\displaystyle -1.060 = - 1,564 \cos A$

$\displaystyle \frac{-1.060 }{- 1,564}= \frac{- 1,564 \cos A}{- 1,564}$

$\displaystyle \cos A \approx 0.6777$

Taking the inverse cosine:

$\displaystyle A = \cos ^{-1} 0.6777 \approx 47 ^{\circ }$,

the correct response.

Recall that $\displaystyle sin(\frac{\pi}{6}) =0.5$.

Therefore, we are looking for $\displaystyle sin(8*\frac{\pi}{6})$ or $\displaystyle sin(\frac{4\pi}{3})$.

Now, this has a reference angle of $\displaystyle \frac{\pi}{3}$, but it is in the third quadrant. This means that the value will be negative. The value of $\displaystyle sin(\frac{\pi}{3})$ is $\displaystyle \frac{\sqrt{3}}{2}$. However, given the quadrant of our angle, it will be $\displaystyle -\frac{\sqrt{3}}{2}$.