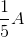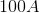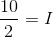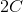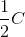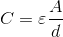Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Physics : Electricity

Study concepts, example questions & explanations for SAT II Physics

Create An Account

All SAT II Physics Resources

45 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Electric Circuits

If a circuit contains a 10V $\displaystyle 10V$ battery and a $2\Omega$ $\displaystyle 2\Omega$ resistor what is the current of the circuit?

Possible Answers:

$\frac{1}{5}A$ $\displaystyle \frac{1}{5}A$

20A $\displaystyle 20A$

100A $\displaystyle 100A$

40A $\displaystyle 40A$

$\displaystyle 5A$

Correct answer:

$\displaystyle 5A$

Explanation:

Ohm's law states:

V=IR $\displaystyle V=IR$

Where $\displaystyle V$ is voltage, $\displaystyle I$ is current, and $\displaystyle R$ is resistance.

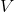
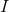
We can substitute the given values from the question into the equation and solve:

10=I(2) $\displaystyle 10=I(2)$

$\frac{10}{2}=I$ $\displaystyle \frac{10}{2}=I$

5=I $\displaystyle 5=I$

Report an Error

Example Question #41 : Electricity And Magnetism

There are three resistors in parallel in a circuit with resistances of $10\Omega$ $\displaystyle 10\Omega$, $20\Omega$ $\displaystyle 20\Omega$, and $30\Omega$ $\displaystyle 30\Omega$.

What is the equivalent resistance?

Possible Answers:

$1\Omega$ $\displaystyle 1\Omega$

$5.45\Omega$ $\displaystyle 5.45\Omega$

$0.017\Omega$ $\displaystyle 0.017\Omega$

$6000\Omega$ $\displaystyle 6000\Omega$

$60\Omega$ $\displaystyle 60\Omega$

Correct answer:

$5.45\Omega$ $\displaystyle 5.45\Omega$

Explanation:

The equation for resistors in parallel is:

$\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}...$ $\displaystyle \frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}...$

We are given the values of the resistors. Using this formula, we can solve for the equivalent resistance.

Plug in the given values and solve.

$\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}...$ $\displaystyle \frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}...$

$\frac{1}{R_{eq}}=\frac{1}{10\Omega}+\frac{1}{20\Omega}+\frac{1}{30\Omega}...$ $\displaystyle \frac{1}{R_{eq}}=\frac{1}{10\Omega}+\frac{1}{20\Omega}+\frac{1}{30\Omega}...$

$\frac{1}{R_{eq}}=\frac{11}{60\Omega}$ $\displaystyle \frac{1}{R_{eq}}=\frac{11}{60\Omega}$

$R_{eq}=\frac{60\Omega}{11}$ $\displaystyle R_{eq}=\frac{60\Omega}{11}$

$R_{eq}=5.45\Omega$ $\displaystyle R_{eq}=5.45\Omega$

Report an Error

Example Question #1 : Resistors

A voltage of $\displaystyle 6V$ applied between the ends of a wire results in a current of 60A $\displaystyle 60A$. What is the resistance of the wire?

Possible Answers:

$0.2\Omega$ $\displaystyle 0.2\Omega$

$1\Omega$ $\displaystyle 1\Omega$

$5\Omega$ $\displaystyle 5\Omega$

$10\Omega$ $\displaystyle 10\Omega$

$0.1\Omega$ $\displaystyle 0.1\Omega$

Correct answer:

$0.1\Omega$ $\displaystyle 0.1\Omega$

Explanation:

This question can be solved using Ohm's law:

V=IR $\displaystyle V=IR$

We are given the voltage and the current. Using these values, we can solve for the resistance.

$\displaystyle 6V=(60A)R$

$R=\frac{6V}{60A}=0.1\Omega$ $\displaystyle R=\frac{6V}{60A}=0.1\Omega$

Report an Error

Example Question #2 : Electricity And Magnetism

A capacitor with capacitance 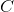$\displaystyle C$ is constructed by putting a thin piece of cardboard between two copper plates, then each plate is connected to a battery. If the copper plates are cut in half then what is the effect on the capacitance of the circuit?

Possible Answers:

$C^{2}$ $\displaystyle C^{2}$

$\frac{1}{C}$ $\displaystyle \frac{1}{C}$

$\frac{1}{2}C$ $\displaystyle \frac{1}{2}C$

$\displaystyle 2C$

$\displaystyle C$

Correct answer:

$\frac{1}{2}C$ $\displaystyle \frac{1}{2}C$

Explanation:

Capacitance of a circuit is defined by the equation:

$C=\varepsilon\frac{A}{d}$ $\displaystyle C=\varepsilon\frac{A}{d}$

Where $\displaystyle C$ is the capacitance, $\varepsilon$ $\displaystyle \varepsilon$ is a constant of nature, $\displaystyle A$ is the area of the capacitor, and $\displaystyle d$ is the distance between the two plates

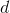
Since the metal plates are cut in half, the area is halved. We can substitute $\frac{1}{2}A$ $\displaystyle \frac{1}{2}A$ in for $\displaystyle A$

The result is that the capacitance is half the original quantity.

Report an Error

Example Question #1 : Coulomb's Law

If the distance between two charged particles is doubled, the strength of the electric force between them will __________.

Possible Answers:

quadruple

be quartered

double

remain unchanged

be halved

Correct answer:

be quartered

Explanation:

Coulomb's law gives the relationship between the force of an electric field and the distance between two charges:

$F_e=k\frac{q_1q_2}{r^2}$ $\displaystyle F_e=k\frac{q_1q_2}{r^2}$

The strength of the force will be inversely proportional to the square of the distance between the charges.

When the distance between the charges is doubled, the total force will be divided by four (quartered).

$F_e=k\frac{q_1q_2}{(2r)^2}=k\frac{q_1q_2}{4r^2}=\frac{1}{4}(k\frac{q_1q_2}{r^2})$ $\displaystyle F_e=k\frac{q_1q_2}{(2r)^2}=k\frac{q_1q_2}{4r^2}=\frac{1}{4}(k\frac{q_1q_2}{r^2})$

Report an Error

Example Question #1 : Electric Potential Energy

On which of the following does the amount of work required to move a charge in an electric field depend?

Possible Answers:

Only the magnetic field

Only the path traveled

Neither the potential nor the path traveled

Both the potential and the path traveled

Only the change in potential

Correct answer:

Only the change in potential

Explanation:

Work done by electric field is defined:

$W=-\Delta PE$ $\displaystyle W=-\Delta PE$

Notice that the only variable in the equation is the potential, so this is the only quantity on which work depends.

Report an Error

View SAT Subject Test in Physics Tutors

Robert
Certified Tutor

Daytona State College, Bachelor in Arts, Teaching English as a Second Language (ESL).

View SAT Subject Test in Physics Tutors

Jacqueline
Certified Tutor

Yale University, Bachelor of Science, German Studies. Cornell University, Master of Science, German Studies.

View SAT Subject Test in Physics Tutors

Evgenii
Certified Tutor

All SAT II Physics Resources

45 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Dallas Fort Worth, ISEE Tutors in Dallas Fort Worth, LSAT Tutors in Atlanta, Computer Science Tutors in Phoenix, Statistics Tutors in San Diego, Computer Science Tutors in Miami, Reading Tutors in Miami, Biology Tutors in Houston, Spanish Tutors in Philadelphia, Math Tutors in Phoenix

Popular Courses & Classes

MCAT Courses & Classes in Chicago, MCAT Courses & Classes in Seattle, Spanish Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Atlanta, GRE Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Atlanta, GMAT Courses & Classes in New York City, Spanish Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Atlanta, ACT Courses & Classes in Phoenix

Popular Test Prep

GRE Test Prep in New York City, SAT Test Prep in San Diego, ISEE Test Prep in Dallas Fort Worth, GRE Test Prep in Phoenix, GMAT Test Prep in Miami, LSAT Test Prep in Dallas Fort Worth, GRE Test Prep in Atlanta, GRE Test Prep in Dallas Fort Worth, ACT Test Prep in Miami, GMAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Physics : Electricity

Study concepts, example questions & explanations for SAT II Physics

All SAT II Physics Resources

Example Questions

Example Question #1 : Electric Circuits

Example Question #41 : Electricity And Magnetism

Example Question #1 : Resistors

Example Question #2 : Electricity And Magnetism

Example Question #1 : Coulomb's Law

Example Question #1 : Electric Potential Energy

All SAT II Physics Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: