All SAT Math Resources
Example Questions
Example Question #1 : Squaring / Square Roots / Radicals
Simplify:
If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:
Example Question #1 : Squaring / Square Roots / Radicals
Simplify the radical.
We can break the square root down into 2 roots of 67 and 49. 49 is a perfect square and reduces to 7.
Example Question #2 : Squaring / Square Roots / Radicals
Simplify:
If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:
Example Question #64 : Exponents
x2 = 36
Quantity A: x
Quantity B: 6
Quantity B is greater
Quantity A is greater
The two quantities are equal
The relationship cannot be determined from the information given
The relationship cannot be determined from the information given
x2 = 36 -> it is important to remember that this leads to two answers.
x = 6 or x = -6.
If x = 6: A = B.
If x = -6: A < B.
Thus the relationship cannot be determined from the information given.
Example Question #2 : Squaring / Square Roots / Radicals
According to Heron's Formula, the area of a triangle with side lengths of a, b, and c is given by the following:
where s is one-half of the triangle's perimeter.
What is the area of a triangle with side lengths of 6, 10, and 12 units?
8√14
4√14
48√77
14√2
12√5
8√14
We can use Heron's formula to find the area of the triangle. We can let a = 6, b = 10, and c = 12.
In order to find s, we need to find one half of the perimeter. The perimeter is the sum of the lengths of the sides of the triangle.
Perimeter = a + b + c = 6 + 10 + 12 = 28
In order to find s, we must multiply the perimeter by one-half, which would give us (1/2)(28), or 14.
Now that we have a, b, c, and s, we can calculate the area using Heron's formula.
Example Question #181 : New Sat
Simplify the radical expression.
Look for perfect cubes within each term. This will allow us to factor out of the radical.
Simplify.
Example Question #171 : Exponents
Simplify the expression.
Use the distributive property for radicals.
Multiply all terms by 
Combine terms under radicals.
Look for perfect square factors under each radical. 


Since both radicals are the same, we can add them.
Example Question #3 : Squaring / Square Roots / Radicals
Which of the following expression is equal to
When simplifying a square root, consider the factors of each of its component parts:
Combine like terms:
Remove the common factor, 
Pull the 


Example Question #1 : Squaring / Square Roots / Radicals
Which of the following is equal to the following expression?
First, break down the components of the square root:
Combine like terms. Remember, when multiplying exponents, add them together:
Factor out the common factor of 
Factor the 
Combine the factored 

Now, you can pull 

Example Question #4 : Squaring / Square Roots / Radicals
Which of the following expressions is equal to the following expression?
First, break down the component parts of the square root:
Combine like terms in a way that will let you pull some of them out from underneath the square root symbol:
Pull out the terms with even exponents and simplify:
Certified Tutor
Certified Tutor
All SAT Math Resources

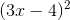

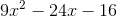
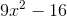




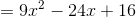

















![\sqrt[3]{-64x^{6}y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26625/gif.latex)




![\sqrt[3]{-64}*\sqrt[3]{x^6}*\sqrt[3]{y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/85063/gif.latex)
![\sqrt[3]{-4*-4*-4}*\sqrt[3]{x^2*x^2*x^2}*\sqrt[3]{y^4*y^4*y^4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/119850/gif.latex)



















































