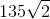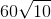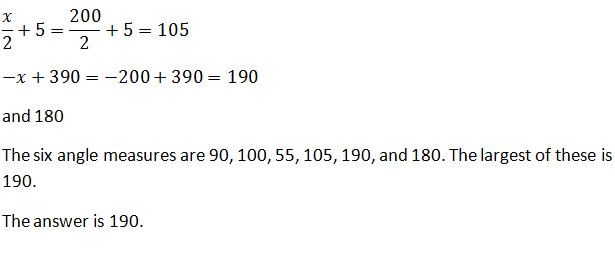All SAT Math Resources
Example Questions
Example Question #1 : Hexagons

Archimedes High School has an unusual track in that it is shaped like a regular hexagon, as above. Each side of the hexagon measures 264 feet.
Alvin runs at a steady speed of seven miles an hour for twelve minutes, starting at point A and working his way clockwise. When he is finished, which of the following points is he closest to?
Point E
Point D
Point C
Point B
Point F
Point E
Alvin runs at a rate of seven miles an hour for twelve minutes, or 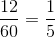


One mile comprises 5,280 feet, so this is equal to
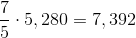
Since each side of the track measures 264 feet, this means that Alvin runs


which means that Alvin runs around the track four complete times, plus four more sides of the track. Alvin stops when he is at Point E.
Example Question #2 : How To Find The Perimeter Of A Hexagon
A circle with circumference 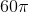
None of these
Below is the figure referenced; note that the hexagon is divided by its diameters, and that an apothem—a perpendicular bisector from the center to one side—has been drawn.

The circle has circumference 



The hexagon is divided into six equilateral triangles. One, 








this makes the perimeter of the hexagon six times this, or

Example Question #2 : Hexagons
How many diagonals are there in a regular hexagon?
A diagonal is a line segment joining two non-adjacent vertices of a polygon. A regular hexagon has six sides and six vertices. One vertex has three diagonals, so a hexagon would have three diagonals times six vertices, or 18 diagonals. Divide this number by 2 to account for duplicate diagonals between two vertices. The formula for the number of vertices in a polygon is:
where 
Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon
How many diagonals are there in a regular hexagon?
10
6
18
9
3
9
A diagonal connects two non-consecutive vertices of a polygon. A hexagon has six sides. There are 3 diagonals from a single vertex, and there are 6 vertices on a hexagon, which suggests there would be 18 diagonals in a hexagon. However, we must divide by two as half of the diagonals are common to the same vertices. Thus there are 9 unique diagonals in a hexagon. The formula for the number of diagonals of a polygon is:
where n = the number of sides in the polygon.
Thus a pentagon thas 5 diagonals. An octagon has 20 diagonals.
Example Question #19 : Geometry
Hexagon 



Below is the referenced hexagon, with some additional segments constructed.

Note that the segments 














and
For the same reason, 
By the Pythagorean Theorem,

Example Question #21 : Geometry

The provided image represents a track in the shape of a regular hexagon with perimeter one fourth of a mile.
Teresa starts at Point A and runs clockwise until she gets halfway between Point E and Point F. How far does she run, in feet?
One mile is equal to 5,280 feet; one fourth of a mile is equal to

Each of the six congruent sides measures one sixth of this, or
Teresa runs clockwise from Point A to halfway between Point E and Point F, so she runs along four and one half sides, for a total of

Example Question #1 : Hexagons
200
210
180
190
170
Example Question #21 : Plane Geometry
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
The sum of the interior angles of a polygon is given by 

Example Question #1 : Hexagons
Find the sum of all the inner angles in a hexagon.
To solve, simply use the formula to find the total degrees inside a polygon, where n is the number of vertices.
In this particular case, a hexagon means a shape with six sides and thus six vertices.
Thus,
Example Question #1 : How To Find The Area Of A Hexagon
An equilateral triangle with side length 
Because it can be split into two 
With that in mind, the equilateral triangle in question has area of 
Now consider that a regular hexagon can be split into six congruent equilateral triangles with a vertex at the center and the side opposite the center as one of the hexagon's sides (a handy way of finding a hexagon's area if you can't use the regular polygon formula requiring an apothem.) Knowing that, our answer is 
Certified Tutor
All SAT Math Resources