SSAT Middle Level Math : How to find the area of a rectangle
Study concepts, example questions & explanations for SSAT Middle Level Math
All SSAT Middle Level Math Resources
Example Questions
Example Question #241 : Geometry
Steve's bedroom measures 20' by 18' by 8' high. He wants to paint the ceiling and all four walls using a paint that gets 360 square feet of coverage per gallon. A one-gallon can of the paint Steve wants costs $36.00; a one-quart can costs $13.00. What is the least amount of money that Steve can expect to spend on paint in order to paint his room?
Two of the walls have area 
Therefore, the total area Steve wants to cover is
Divide 968 by 360 to get the number of gallons Steve needs to paint his bedroom:
Since 
The first option will cost him 
Example Question #51 : Quadrilaterals
Give the area of the rectangle in the above diagram.
The area of a rectangle is the product of its length and its height:
The rectangle has a perimeter of 80.64 square centimeters.
Example Question #52 : Quadrilaterals
Give the area of the rectangle in the above diagram.
The area of a rectangle is the product of its length and its width:
The area of the rectangle is 42 square inches.
Example Question #242 : Geometry
Give the surface area of the above box in square centimeters.
100 centimeters make one meter, so convert each of the dimensions of the box by multiplying by 100.
Use the surface area formula, substituting 
Example Question #4 : Geometry
Above is a figure that comprises a red square and a white rectangle. The ratio of the length of the white rectangle to the sidelength of the square is 
To make this easier, we will assume that the rectangle has length 5 and the square has sidelength 3. Then the area of the entire figure is
and the area of the square is
The square, therefore, takes up
of the entire figure.
Example Question #91 : Plane Geometry
The rectangle above is 
Note: Figure not drawn to scale.
The area of the rectangle is 
Example Question #1 : How To Find The Area Of A Rectangle
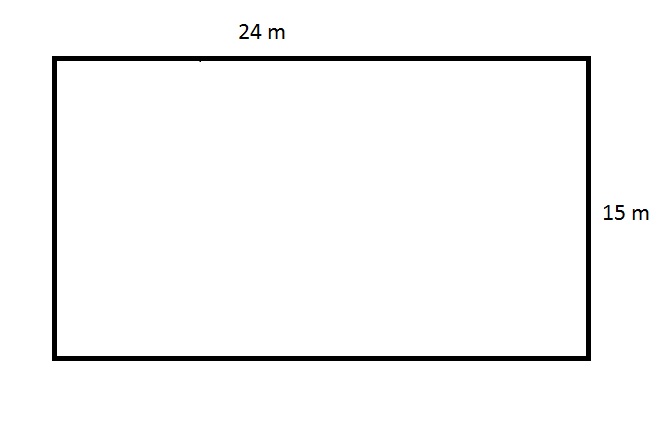
The above depicts a rectangular swimming pool for an apartment. The pool is two meters deep everywhere. What is the volume of the pool in cubic meters?
The correct answer is not among the other choices.
The pool can be seen as a rectangular prism with dimensions 24 meters by 15 meters by 2 meters; its volume is the product of these dimensions, or
Example Question #5 : Geometry
Note: Figure NOT drawn to scale.
What percent of the above figure is white?
The large rectangle has length 80 and width 40, and, consequently, area
The white region is a rectangle with length 30 and width 20, and, consequently, area
The white region is
of the large rectangle.
Example Question #1 : How To Find The Area Of A Rectangle
What is the area of a rectangle with length 
The formula for the area, 
To calculate this area, just multiply the two terms.
Example Question #321 : Ssat Middle Level Quantitative (Math)
Order the following from least area to greatest area:
Figure A: A rectangle with length 10 inches and width 14 inches.
Figure B: A square with side length 1 foot.
Figure C: A triangle with base 16 inches and height 20 inches.
Figure A has area 
Figure B has area 
Figure C has area 
The figures, arranged from least area to greatest, are A, B, C.
Certified Tutor
Certified Tutor
All SSAT Middle Level Math Resources
