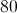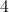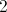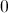We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Algebra

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Ssat Upper Level Quantitative (Math)

Find the sum of this infinite geometric series:

$4 + \frac{7}{2} + \frac{49}{16} + ... + 4 \cdot \left ( \frac {7}{8} \right ) ^{n}+...$

Possible Answers:

Correct answer:

Explanation:

The sum of an infinite series with first term and common ratio is

$S = \frac{a}{1-r}$

Set $a=4,r= \frac{7}{8}$ , and evaluate:

$S = \frac{a}{1-r} = \frac{4}{1-\frac{7}{8}} = \frac{4}{\left ( \frac{1}{8}\right )} = 4 \cdot 8=32$

Report an Error

Example Question #2 : Ssat Upper Level Quantitative (Math)

Give the next number in the following sequence:

3, 5, 10, 12, 24, 26, 52, 54, _____

Possible Answers:

108

102

104

Correct answer:

108

Explanation:

The sequence is generated by alternately adding 2, then multiplying by 2:

3 + 2= 5

$5 \times 2 = 10$

10+2 = 12

$12 \times 2 = 24$

24 + 2 = 26

$26 \times 2 = 52$

52 + 2 = 54

$54 \times 2 = \underline{108}$ , which is the correct choice.

Report an Error

Example Question #3 : Ssat Upper Level Quantitative (Math)

Define an operation on the real numbers as follows:

$a \bigtriangleup b = 3a - 2b$

Find the value of that makes this statement true:

$x\bigtriangleup 5 = 32$

Possible Answers:

$x = 20 \frac{2}{3}$

$x = 7\frac{1}{3}$

There is no such value of .

$x = \frac{2}{3}$

x= 14

Correct answer:

x= 14

Explanation:

Replace a=x, b=5 in the defintiion:

$a \bigtriangleup b = 3a - 2b$

$x\bigtriangleup 5 =3x - 2 \cdot 5$

$x\bigtriangleup 5 =3x - 10$

Now, set this equal to 32 and solve for :

$x\bigtriangleup 5 = 32$

3x - 10 = 32

3x - 10 + 10= 32+ 10

3x = 42

$3x \div 3= 42 \div 3$

x= 14

Report an Error

Example Question #4 : Ssat Upper Level Quantitative (Math)

What number replaces the circle?

$1, 1, 2, 4, 6, 18, 21, 84, 88, \square, \bigcirc...$

Possible Answers:

440

465

445

357

352

Correct answer:

445

Explanation:

The sequence is formed by alternately multiplying by a number, then adding the same number; the number incrementally increases every other term.

$1 \times 1 = 1$

1 + 1 = 2

$2 \times 2 = 4$

4 + 2 = 6

$6 \times 3 = 18$

18 + 3 = 21

$21 \times4 = 84$

84 + 4 = 88

$88 \times 5 = 440$ , the number which replaces the square.

440 + 5 = 445 , the number which replaces the circle.

Report an Error

Example Question #5 : Ssat Upper Level Quantitative (Math)

$\left \lfloor N \right \rfloor$ is defined as the greatest integer less than or equal to .

Evaluate the expression for x = 0.7 :

$\left \lfloor 2x +0.5 \right \rfloor + \left \lfloor 3x +0.2\right \rfloor$

Possible Answers:

4.2

5.2

Correct answer:

Explanation:

Substitute:

$\left \lfloor 2x +0.5 \right \rfloor + \left \lfloor 3x +0.2\right \rfloor$

$= \left \lfloor 2 \cdot 0.7 +0.5 \right \rfloor + \left \lfloor 3 \cdot 0.7 +0.2\right \rfloor$

$= \left \lfloor 1.4 +0.5 \right \rfloor + \left \lfloor 2.1 +0.2\right \rfloor$

$= \left \lfloor 1.9\right \rfloor + \left \lfloor 2.3\right \rfloor$

=1+2 = 3

Report an Error

Example Question #6 : Ssat Upper Level Quantitative (Math)

$\left \lceil N\right \rceil$ is defined as the least integer greater than or equal to .

Evaluate for x = 0.8 :

$\left \lceil 4 x -0.4 \right \rceil + 5x+ 0.3$

Possible Answers:

6.3

7.3

Correct answer:

7.3

Explanation:

Substitute x = 0.8 :

$\left \lceil 4 x -0.4 \right \rceil + 5x+ 0.3$

$= \left \lceil 4 \cdot 0.8 -0.4 \right \rceil + 5 \cdot 0.8 + 0.3$

$= \left \lceil 3.2 -0.4 \right \rceil + 4 + 0.3$

$= \left \lceil 2.8 \right \rceil + 4 + 0.3$

=3 + 4 + 0.3 = 7.3

Report an Error

Example Question #7 : Ssat Upper Level Quantitative (Math)

What number replaces the circle in this sequence?

$\bigcirc , \square , 8, 6, 12, 10, 20, 18, 36....$

Possible Answers:

Correct answer:

Explanation:

This sequence is alternately generated by subtracting two and multiplying by two.

We can therefore find the numbers that replace the square and the circle by reversing the pattern - alternately dividing by two and adding two beginning at 36:

$36 \div 2 = 18$

18 + 2 = 20

$20 \div 2 =10$

10 + 2 = 12

$12 \div 2 = 6$

6 + 2 = 8

$8 \div 2 = 4$ - this replaces the circle

4+2=6 - this replaces the square

Report an Error

Example Question #8 : Ssat Upper Level Quantitative (Math)

In the following number sequence, what number goes in place of the circle?

$1, 9, 25, 49, 81, 121, \bigcirc...$

Possible Answers:

144

169

161

141

196

Correct answer:

169

Explanation:

The sequence comprises the squares of the odd integers, in order:

$1^{2} = 1$

$3^{2} = 9$

...

$11^{2} = 121$

The next number, which replaces the circle, is

$13^{2} = 169$ .

Report an Error

Example Question #9 : Ssat Upper Level Quantitative (Math)

Define an operation on the set of real numbers as follows:

$a\; \S\; b = a^{2} + b ^{2}$

Evaluate:

$-4\; \S\; \left ( -5 \right )$

Possible Answers:

The expression is undefined.

Correct answer:

Explanation:

$a\; \S\; b = a^{2} + b ^{2}$

$-4\; \S\; \left ( -5 \right ) = \left ( -4 \right )^{2} + \left ( -5\right ) ^{2}$

$= \left ( -4 \right )\times \left ( -4 \right ) + \left ( -5\right ) \times \left ( -5 \right )$

= 16 +25 = 41

Report an Error

Example Question #10 : Ssat Upper Level Quantitative (Math)

In the following number sequence, what number goes in place of the circle?

$20, 10, 16, 8, 14, 7, \square, \bigcirc...$

Possible Answers:

$6\frac{1}{2}$

$9\frac{1}{2}$

$11\frac{1}{2}$

$10\frac{1}{2}$

$7\frac{1}{2}$

Correct answer:

$6\frac{1}{2}$

Explanation:

The sequence is generated by alternately dividing by 2 and adding 6:

$20 \div 2 = 10$

10 + 6 = 16

$16 \div 2 = 8$

8 + 6 = 14

$14 \div 2 = 7$

7 + 6 = 13 - This number replaces the square.

$13\div 2 = 6\frac{1}{2}$ - This number replaces the circle.

Report an Error

View SSAT- Upper Level Tutors

Rose
Certified Tutor

Texas A & M University-Corpus Christi, Associate in Science, Elementary School Teaching. Walden University, Masters in Educat...

View SSAT- Upper Level Tutors

Kevin
Certified Tutor

St. Johns University, Bachelors, Math/Coaching.

View SSAT- Upper Level Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Phoenix, LSAT Tutors in Denver, ISEE Tutors in Denver, Algebra Tutors in Boston, Spanish Tutors in Washington DC, GMAT Tutors in Dallas Fort Worth, GMAT Tutors in Seattle, GRE Tutors in Miami, English Tutors in Seattle, ACT Tutors in Phoenix

Popular Courses & Classes

MCAT Courses & Classes in San Diego, SSAT Courses & Classes in New York City, ISEE Courses & Classes in Los Angeles, SAT Courses & Classes in Philadelphia, Spanish Courses & Classes in New York City, MCAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Atlanta, ACT Courses & Classes in Houston, LSAT Courses & Classes in Philadelphia

Popular Test Prep

GRE Test Prep in Atlanta, GMAT Test Prep in Washington DC, MCAT Test Prep in San Diego, LSAT Test Prep in San Diego, ISEE Test Prep in Atlanta, SSAT Test Prep in Houston, SAT Test Prep in Dallas Fort Worth, SSAT Test Prep in New York City, SSAT Test Prep in Boston, MCAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Algebra

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #1 : Ssat Upper Level Quantitative (Math)

Example Question #2 : Ssat Upper Level Quantitative (Math)

Example Question #3 : Ssat Upper Level Quantitative (Math)

Example Question #4 : Ssat Upper Level Quantitative (Math)

Example Question #5 : Ssat Upper Level Quantitative (Math)

Example Question #6 : Ssat Upper Level Quantitative (Math)

Example Question #7 : Ssat Upper Level Quantitative (Math)

Example Question #8 : Ssat Upper Level Quantitative (Math)

Example Question #9 : Ssat Upper Level Quantitative (Math)

Example Question #10 : Ssat Upper Level Quantitative (Math)

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: