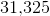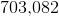Let the middle integer of the three be . The three integers are therefore 

, and they can be found using the equation

The three even integers are therefore 306, 308, and 310, and the product of the least and greatest of these is 

Let the middle integer of the three be . The three integers are therefore 

, and they can be found using the equation

The three integers are 177, 179, and 181, and the product of the least and greatest is 

Call the least of the four integers . The four integers are therefore

,

and they can be found using the equation

The integers are 836, 837, 838, 839. 

To get the correct response, multiply: 

Let the middle integer of the three be . The three integers are therefore 

, and they can be found using the equation

This contradicts the condition that the numbers are integers. Therefore, three integers satisfying the given conditions cannot exist. 

Let the middle integer of the three be . The three integers are therefore 

, and they can be found using the equation

The integers are therefore 103, 104, 105. The correct response is their product, which is

This is a geometric sequence since the pattern of the sequence is through multiplication.  

You have to multiple each value by  to get the next one.  

The value before  is  so .

Let , , , and  be the four consecutive integers. Then their sum would be 

In other words, if 6 were to be subtracted from their sum, the difference would be a multiple of 4. Therefore, we subtract 6 from each of the choices and see if any of the resulting differences are multiples of 4.

Since this only happens in the case of 178, this is the only number of the four that can be a sum of four consecutive integers: 43, 44, 45, 46.

The easiest way to solve this problem is to write out the first few numbers of the sets. 

Set R (multiples of 4): 

Set W (multiples of 8): 

Set X (multiples of 2): 

Set Y (multiples of 6): 

Set Z (multiples of 1): 

Set Q (multiples of 7): 

Given that Set W is the only set in which the entire set of numbers is reflected in Set R, it is the correct answer. 

Determining sequences can take some trial and error, but generally aren't as intimidating as they may at first appear. For this sequence, you multiply the first term by 3, and then subtract 3 two times in a row. Then repeat. When you get to 33, you have only subtracted 3 once, so you have to do that one more time:

In order to find the next number in the sequence, take a look at the patterns and common differences between the existing numbers in the sequence. Starting with , we add  to get , subtract  to get , and then repeat. 

When we get to  for the second time in the sequence, we are adding  to get . By the next step in the sequence, we will subtract  to get the missing number .