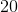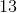We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

TACHS Math : Geometry

Study concepts, example questions & explanations for TACHS Math

Create An Account

All TACHS Math Resources

43 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Perimeter Of Triangles, Squares, And Rectangles

Find the perimeter of a square with the following side length:

s=5

Possible Answers:

625

Correct answer:

Explanation:

Perimeters can be calculated by adding together the side lengths of a polygon. A square has four sides that are all the same length, therefore, we can write the following formula to solve for the perimeter.

P=s+s+s+s

We can rewrite this equation as the following:

P=4s

In these equations the variable, , represents side length.

Substitute the known side length and solve.

$P=4\times5$

P=20

Report an Error

Example Question #23 : Math

Find the circumference of a circle with the following radius:

r=4

Possible Answers:

$16\pi$

$\pi$

$4\pi$

3.14

$8\pi$

Correct answer:

$8\pi$

Explanation:

In order to find the circumference of a circle we will use the following formula:

$C=2\pi r$

In this equation, the variable, , represent's the circle's radius.

Substitute in for the circle's radius.

$C=2\times\pi \times 4$

Simplify and solve.

$C=8\pi$

Report an Error

Example Question #1 : Area Of Squares And Rectangles

A square has perimeter 24 feet. Give its area.

Possible Answers:

36 square feet

144 square feet

18 square feet

576 square feet

Correct answer:

36 square feet

Explanation:

The perimeter of a figure is the sum of the lengths of its sides. A square comprises four sides of equal length, so, if the perimeter of the square is 24 feet, then each side has length

$24 \div 4 = 6$ feet.

The area of the square is equal to the length of a side multiplied by itself, so the area of this square is

$6\times6= 36$ square feet.

Report an Error

Example Question #2 : Geometry

Jennifer wants to wallpaper her room which is made up for four rectangular walls each measuring at feet by feet. If each roll of wallpaper covers square feet of space, how many rolls of wallpaper will Jennifer need?

Possible Answers:

Correct answer:

Explanation:

Start by finding out the total square footage of wallpaper needed.

Find the area of one wall. Recall that in order to find the area of a rectangle, you must multiply the length by the width.

$\text{Area of One Wall}=15 \times 12=180$

Since we have four identical walls,

$\text{Total Area of Walls}=4 \times 180 =720$

Now divide this by the amount of square feet covered by each roll of wallpaper to find how many rolls are needed.

$\text{Rolls of wallpaper needed}=\frac{720}{60}=12$

Report an Error

Example Question #1 : Area Of A Circle

Find the area of a circle with the following radius:

r=7

Possible Answers:

$49\pi$

$14\pi$

$7\pi$

$48\pi$

$16\pi$

Correct answer:

$49\pi$

Explanation:

The area of a circle can be calculated using the following formula:

$A=\pi r^2$

In this formula the radius is denoted by the variable, .

Substitute in the known variables and solve for the circle's area.

$A=\pi \times 7^2$

$A=49\pi$

Report an Error

Example Question #33 : Tachs: Math And Ability

Which is equal to the radius of a circle with area $400 \pi$

Possible Answers:

100

200

Correct answer:

Explanation:

The formula for the area of a circle, given its radius , is $A = \pi r^{2}$ . Replace with $400 \pi$ :

$\pi r^{2} = 400 \pi$

To find the radius , first, divide both sides by $\pi$ :

$\frac{\pi r^{2}}{\pi} = \frac{400 \pi}{\pi}$

$r^{2} = 400$

Now, find the square root of both sides. Since $400 = 20 \times 20$ , 20 is the square root of 400, so

r = 20 .

The radius of the given circle is 20.

Report an Error

Example Question #1 : Area

To determine whether a machine on an assembly line is filling bottles with the correct amount of soda, twenty bottles are selected. The tenth bottle and every tenth bottle after that are taken off the line and examined.

This is an example of which kind of sampling?

Possible Answers:

Convenience sampling

Systematic sampling

Stratified sampling

Cluster sampling

Correct answer:

Systematic sampling

Explanation:

The sample in this scenario is selected from the population by choosing obects that occur at regular intervals. That makes this an example of systematic sampling.

Report an Error

Example Question #1 : Area

What is the area of a circle that has a diameter of ?

Possible Answers:

92.6

37.7

452.4

113.1

Correct answer:

113.1

Explanation:

Recall how to find the area of a circle:

$\text{Area of Circle}=\pi \times \text{radius}^2$

To find the length of the radius, divide the diameter by two.

$\text{radius}=\frac{12}{2}=6$

Now, plug it into the equation for the area of a circle.

$\text{Area of Circle}=\pi \times 6^2=36\pi=113.1$

Report an Error

Example Question #1 : Volume

Calculate the volume of a sphere with the following radius:

r=3

Possible Answers:

$16 \pi$

$36\pi$

$33\pi$

$24\pi$

$8\pi$

Correct answer:

$36\pi$

Explanation:

We can calculate the the volume of a sphere using the following formula:

$V=\frac{4}{3}\pi r^3$

in this formula the variable, , represents the radius of the sphere.

Substitute in the known radius and calculate the volume.

$V=\frac{4}{3}\times \pi \times 3^3$

$V=\frac{4}{3}\times \pi \times 27$

$V=\frac{4}{3}\times 27\pi$

Simplify.

$V=\frac{4}{3}\times \frac{27\pi}{1}$

$V=\frac{108\pi}{3}$

Solve.

$V=36\pi$

Report an Error

View Tutors

Tyler
Certified Tutor

University of Illinois at Urbana-Champaign, Bachelor of Science, Physics.

View Tutors

Nina
Certified Tutor

The University of Texas at Austin, Bachelor in Arts, Finance.

View Tutors

Mohini
Certified Tutor

Indian School of Business, Masters in Business Administration, Marketing.

All TACHS Math Resources

43 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Phoenix, SAT Tutors in Phoenix, English Tutors in Houston, LSAT Tutors in Chicago, English Tutors in Seattle, ACT Tutors in Houston, LSAT Tutors in San Diego, GRE Tutors in Boston, Algebra Tutors in San Diego, ISEE Tutors in Atlanta

Popular Courses & Classes

ACT Courses & Classes in Atlanta, ACT Courses & Classes in Seattle, GRE Courses & Classes in Chicago, SSAT Courses & Classes in San Diego, LSAT Courses & Classes in Houston, SAT Courses & Classes in Denver, ACT Courses & Classes in New York City, ACT Courses & Classes in Los Angeles, GRE Courses & Classes in Denver, GMAT Courses & Classes in San Diego

Popular Test Prep

MCAT Test Prep in Philadelphia, GRE Test Prep in Denver, MCAT Test Prep in Chicago, SAT Test Prep in Philadelphia, GMAT Test Prep in Chicago, GRE Test Prep in Washington DC, GMAT Test Prep in San Diego, SSAT Test Prep in New York City, ACT Test Prep in Atlanta, GMAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

TACHS Math : Geometry

Study concepts, example questions & explanations for TACHS Math

All TACHS Math Resources

Example Questions

Example Question #1 : Perimeter Of Triangles, Squares, And Rectangles

Example Question #23 : Math

Example Question #1 : Area Of Squares And Rectangles

Example Question #2 : Geometry

Example Question #1 : Area Of A Circle

Example Question #33 : Tachs: Math And Ability

Example Question #1 : Area

Example Question #1 : Area

Example Question #1 : Volume

All TACHS Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: