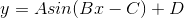The general form for a sine equation is:

The amplitude of a sine equation is the absolute value of .

Since our equation begins with , we would simplify the equation:

The absolute value of  would be .

Amplitude describes the distance from the middle of a periodic function to its local maximum.  covers the range from -1 to 1. Thus, it covers a distance of 2 vertically. Half of this, or 1, gives us the amplitude of the function. It is often helpful to think of the amplitude of a periodic function as its "height". 

The amplitude of a function describes its height from the midline to the maximum. The amplitude of the parent function, , is 1, since it goes from -1 to 1. In this case our function has been multiplied by 4. Think of the effects this multiplication has on the outputs. In , we get our maximum at , and . Here, we will get 4. The same thing happens for our minimum, at  , . Here, we get -4. Thus, by this analysis, it is clear that the amplitude is 4. In the future, remember that the number preceding the cosine function will always be its amplitude.

By definition, the period of a function is the length of  for which it repeats.  starts at 0, continues to 1, goes back to 0, goes to -1, and then back to 0.

This complete cycle goes from  to  .

Recall the form of a sinusoid:

  or     

The important quantities for this question are the amplitude, given by , and period given by  .

For this problem, amplitude is equal to  and period is .

The period of the standard cosine function is .

We can find the period of the given function by dividing  by the coefficient in front of , which is :

.

Giving 

,

where

and 

Then,

,

hence 

.

.

Therefore,

The amplitude of a function is the amount by which the graph of the function travels above and below its midline. When graphing a sine function, the value of the amplitude is equivalent to the value of the coefficient of the sine. Similarly, the coefficient associated with the x-value is related to the function's period. The largest coefficient associated with the sine in the provided functions is 2; therefore the correct answer is .

The amplitude is dictated by the coefficient of the trigonometric function. In this case, all of the other functions have a coefficient of one or one-half.

If we use the standard form of a sine function

the phase shift can be calculated by .  Therefore, in our case, our phase shift is

The first zero can be found by plugging 3π/2 for x, and noting that it is a double period function, the zeros are every π/2, count three back and there is a zero at zero, going down.

A more succinct form for this answer is  but that was not one of the options, so a shifted cosine must be the answer.

The first positive peak is at π/4 at -1, so the cosine function will be shifted π/4 to the right and multiplied by -1. The period and amplitude still 2, so the answer becomes .

To check, plug in π/4 for x and it will come out to -2.