All Abstract Algebra Resources
Example Questions
Example Question #1 : Abstract Algebra
Which of the following is an identity element of the binary operation 
Defining the binary operation 
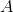


Then there exists an identity element 

Therefore, looking at the possible answer selections the correct answer is,
Example Question #2 : Abstract Algebra
Which of the following illustrates the inverse element?
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every 



Example Question #3 : Abstract Algebra
identify the following definition.
Given 




Subgroup
Cosets
Simple Group
Normal Group
Factor Group
Factor Group
By definition of a factor group it is stated,
Given 






Example Question #1 : Structure Theory
Determine whether the statement is true of false:
True
False
True
This statement is true based on the following theorem.
For all 


If 


Example Question #1 : Principal Ideals
Which of the following is an ideal of a ring?
Minimum Ideal
Prime Ideal
Associative Ideal
Multiplicative Ideal
All are ideals of rings.
Prime Ideal
When dealing with rings there are three main ideals
Proper Ideal: When 




Prime Ideal: When 



Maximal Ideal: When 




Looking at the possible answer selections, Prime Ideal is the correct answer choice.
Example Question #2 : Principal Ideals
Which of the following is an ideal of a ring?
Minimal Ideal
Communicative Ideal
Maximal Ideal
None are ideals
Associative Ideal
Maximal Ideal
When dealing with rings there are three main ideals
Proper Ideal: When 




Prime Ideal: When 



Maximal Ideal: When 




Looking at the possible answer selections, Maximal Ideal is the correct answer choice.
Example Question #3 : Principal Ideals
Which of the following is an ideal of a ring?
Associative Ideal
Proper Ideal
Minimal Ideal
Communicative Ideal
All are ideals
Proper Ideal
When dealing with rings there are three main ideals
Proper Ideal: When 




Prime Ideal: When 



Maximal Ideal: When 




Looking at the possible answer selections, Prime Ideal is the correct answer choice.
Example Question #2 : Abstract Algebra
What definition does the following correlate to?
If 
Principal Ideal Domain
Primitive Field Theorem
Ideals Theorem
Gauss's Lemma
Eisenstein's Irreducibility Criterion
Eisenstein's Irreducibility Criterion
The Eisenstein's Irreducibility Criterion is the theorem for which the given statement is a corollary to.
The Eisenstein's Irreducibility Criterion is as follows.
is a polynomial with coefficients that are integers. If there is a prime number 
Then over the field of rational numbers 
Example Question #3 : Abstract Algebra
Identify the following definition.
For some subfield of 


Plane
Constructible Line
None of the answers.
Line
Angle
Plane
By definition, when 





Example Question #2 : Abstract Algebra
Identify the following definition.
Given that 






Line in
Subfield
Circle in
Plane
Angle
Line in
By definition, given that 







All Abstract Algebra Resources