Defining the binary operation  will help in understanding the identity element. Say  is a set and the binary operator is defined as  for all given pairs in .

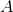
Then there exists an identity element  in  such that given,

Therefore, looking at the possible answer selections the correct answer is,

For every element in a set, there exists another element that when they are multiplied together results in the identity element.

In mathematical terms this is stated as follows.

For every  such that  where  and  is an identity element.

By definition of a factor group it is stated,

Given  is a normal subgroup of , it is denoted that  when the group of left cosets of  in  is called the factor group of  which is determined by .

This statement is true based on the following theorem.

For all ,  in .

If  is a normal subgroup of  then the cosets of  forms a group under the multiplication given by,

When dealing with rings there are three main ideals 

Proper Ideal: When  is a commutative ring, and  is a non empty subset of  then,  is said to have a proper ideal if both the following are true.

 and 

Prime Ideal: When  is a commutative ring,  is a prime ideal if 

 is true and  

Maximal Ideal: When  is a commutative ring, and  is a non empty subset of  then,  has a maximal ideal if all ideal  are 

Looking at the possible answer selections, Prime Ideal is the correct answer choice.

When dealing with rings there are three main ideals 

Proper Ideal: When  is a commutative ring, and  is a non empty subset of  then,  is said to have a proper ideal if both the following are true.

 and 

Prime Ideal: When  is a commutative ring,  is a prime ideal if 

 is true and  

Maximal Ideal: When  is a commutative ring, and  is a non empty subset of  then,  has a maximal ideal if all ideal  are 

Looking at the possible answer selections, Maximal Ideal is the correct answer choice.

When dealing with rings there are three main ideals 

Proper Ideal: When  is a commutative ring, and  is a non empty subset of  then,  is said to have a proper ideal if both the following are true.

 and 

Prime Ideal: When  is a commutative ring,  is a prime ideal if 

 is true and  

Maximal Ideal: When  is a commutative ring, and  is a non empty subset of  then,  has a maximal ideal if all ideal  are 

Looking at the possible answer selections, Prime Ideal is the correct answer choice.

The Eisenstein's Irreducibility Criterion is the theorem for which the given statement is a corollary to.

The Eisenstein's Irreducibility Criterion is as follows.

is a polynomial with coefficients that are integers. If there is a prime number  that satisfy the following,

Then over the field of rational numbers  is said to be irreducible. 

By definition, when  is a subfield of , in the Euclidean plane , the set of all points  that belong to  is called the plane of .

By definition, given that  lives in the Euclidean plane . When elements , , and  in the subfield  , form a straight line who's equation form is , is known as a line in .