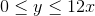To solve the inequality, the first step is to add  to both sides:

The second step is to divide both sides by :

To graph the inequality, you draw a straight number line. Fill in the numbers from  to infinity. Infinity can be designated by a ray. Be sure to fill in the number , since the equation indicated greater than OR equal to.

The graph should look like:

If we plug the points  and  into each equation, we find that these points work only in the equation . This circle has a radius of  and is centered at .

The key here is to look for the line whose slope is the negative reciprocal of the original slope.

In this case,  is the negative reciprocal of .

Therefore, the equation of the line which is perpendicular to the original equation is:

The inverse of a function has all the same points as the original function, except the x values and y values are reversed. The same rule applies to polygons such as triangles.

The simplest way to solve this problem is to plug all of the answer choices into the provided equation, and see which one results in a power of  .  

Alternatively, one could set up the equation,

  and factor, use the quadratic equation, or graph this on a calculator to find the root. 

If we were to factor we would look for factors of c that when added together give us the value in b when we are in the form,

.

In our case . So we need factors of  that when added together give us .

Thus the following factoring would solve this problem.

Then set each binomial equal to zero and solve for v.

Since we can't have a negative power our answer is .

The  inside the argument has the effect of shifting the graph  units to the left. This can be easily seen by graphing both the original and modified functions on a graphing calculator.  

To answer this question, we need to correctly identify where to plug in our given values and solve for .

Points on a graph are written in coordinate pairs. These pairs show the  value first and the  value second. So, for this data:

 means that  is the  value and  is the  value.

We must now plug in our  and  values into the original equation and solve. Therefore:

We can now begin to solve for  by adding up the right side and dividing the entire equation by .

Therefore, the value of  is .

Complex numbers can be represented on the coordinate plane by mapping the real part to the x-axis and the imaginary part to the y-axis.  For example, the expression  can be represented graphically by the point .

Here, we are given the graph and asked to write the corresponding expression.

 not only correctly identifies the x-coordinate with the real part and the y-coordinate with the imaginary part of the complex number, it also includes the necessary . 

 correctly identifies the x-coordinate with the real part and the y-coordinate with the imaginary part of the complex number, but fails to include the necessary .

 misidentifies the y-coordinate with the real part and the x-coordinate with the imaginary part of the complex number.

 misidentifies the y-coordinate with the real part and the x-coordinate with the imaginary part of the complex number.  It also fails to include the necessary .

Complex numbers can be represented on the coordinate plane by mapping the real part to the x-axis and the imaginary part to the y-axis.  For example, the expression  can be represented graphically by the point .

Here, we are given the complex number  and asked to graph it.  We will represent the real part, , on the x-axis, and the imaginary part, , on the y-axis.  Note that the coefficient of  is ; this is what we will graph on the y-axis.  The correct coordinates are .