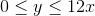All ACT Math Resources
Example Questions
Example Question #1 : How To Graph A Two Step Inequality
Solve and graph the following inequality:
To solve the inequality, the first step is to add 
The second step is to divide both sides by 
To graph the inequality, you draw a straight number line. Fill in the numbers from 

The graph should look like:

Example Question #2 : How To Graph A Two Step Inequality
Points 

If we plug the points 




Example Question #1 : Graphing
Which of the following lines is perpendicular to the line 
The key here is to look for the line whose slope is the negative reciprocal of the original slope.
In this case, 

Therefore, the equation of the line which is perpendicular to the original equation is:
Example Question #1 : How To Graph A Two Step Inequality
Let D be the region on the (x,y) coordinate plane that contains the solutions to the following inequalities:


Which of the following expressions, in terms of 
Example Question #192 : Coordinate Geometry
A triangle is made up of the following points:
What are the points of the inverse triangle?
The inverse of a function has all the same points as the original function, except the x values and y values are reversed. The same rule applies to polygons such as triangles.
Example Question #192 : Graphing
Electrical power can be generated by wind, and the magnitude of power will depend on the wind speed. A wind speed of 





The simplest way to solve this problem is to plug all of the answer choices into the provided equation, and see which one results in a power of 

Alternatively, one could set up the equation,

If we were to factor we would look for factors of c that when added together give us the value in b when we are in the form,

In our case 


Thus the following factoring would solve this problem.
Then set each binomial equal to zero and solve for v.
Since we can't have a negative power our answer is 
Example Question #193 : Graphing
Compared to the graph 







The 

Example Question #1 : How To Graph Complex Numbers
The graph of 



To answer this question, we need to correctly identify where to plug in our given values and solve for 
Points on a graph are written in coordinate pairs. These pairs show the 






We must now plug in our 

We can now begin to solve for 

Therefore, the value of 

Example Question #2 : How To Graph Complex Numbers

Point A represents a complex number. Its position is given by which of the following expressions?
Complex numbers can be represented on the coordinate plane by mapping the real part to the x-axis and the imaginary part to the y-axis. For example, the expression 

Here, we are given the graph and asked to write the corresponding expression.







Example Question #1 : Graphing
Which of the following graphs represents the expression 


Complex numbers cannot be represented on a coordinate plane.



Complex numbers can be represented on the coordinate plane by mapping the real part to the x-axis and the imaginary part to the y-axis. For example, the expression 

Here, we are given the complex number 





Certified Tutor
Certified Tutor
All ACT Math Resources