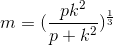Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : How to find the solution to a rational equation with LCD

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #121 : Linear / Rational / Variable Equations

John, Jill, and Jack are splitting a pizza. John eats 1/2 $\displaystyle 1/2$ of the pizza and Jill eats 1/3 $\displaystyle 1/3$ of the pizza. How much of the pizza is left for Jack?

Possible Answers:

1/3 $\displaystyle 1/3$

None $\displaystyle None$

1/6 $\displaystyle 1/6$

1/5 $\displaystyle 1/5$

3/5 $\displaystyle 3/5$

Correct answer:

1/6 $\displaystyle 1/6$

Explanation:

We can write an equation for the amount of pizza eaten, with $\displaystyle x$ as the amount left for Jack.

$\frac{1}{2} + \frac{1}{3} + x = 1$ $\displaystyle \frac{1}{2} + \frac{1}{3} + x = 1$

To solve this equation, we must find the lowest common denominator of 1/2 $\displaystyle 1/2$ and 1/3 $\displaystyle 1/3$. We can list the multiples of $\displaystyle 2$ and $\displaystyle 3$ to find the least common multiple:

$\displaystyle 2: 2, 4, 6, 8, 10, 12, ...$

$\displaystyle 3: 3, 6, 12, 15, 18, 21, ...$

We can see that the least common multiple of $\displaystyle 2$ and $\displaystyle 3$ is $\displaystyle 6$, so we can rewrite each of the fractions with a denominator of $\displaystyle 6$.

$\frac{1}{2}\cdot \frac{3}{3} = \frac{3}{6}$ $\displaystyle \frac{1}{2}\cdot \frac{3}{3} = \frac{3}{6}$

$\frac{1}{3}\cdot \frac{2}{2} = \frac{2}{6}$ $\displaystyle \frac{1}{3}\cdot \frac{2}{2} = \frac{2}{6}$

When we put these fractions back into the equation, we can solve for $\displaystyle x$:

$\frac{3}{6} + \frac{2}{6} + x = 1$ $\displaystyle \frac{3}{6} + \frac{2}{6} + x = 1$

$\frac{5}{6} + x = 1$ $\displaystyle \frac{5}{6} + x = 1$

$x = \frac{1}{6}$ $\displaystyle x = \frac{1}{6}$

Report an Error

Example Question #121 : Equations / Inequalities

What is the slope of a line represented by the equation:

$\displaystyle 15y + 3x = 4$

Possible Answers:

$\frac{1}{5}$ $\displaystyle \frac{1}{5}$

$\frac{4}{3}$ $\displaystyle \frac{4}{3}$

$-\frac{1}{5}$ $\displaystyle -\frac{1}{5}$

$\frac{3}{4}$ $\displaystyle \frac{3}{4}$

Correct answer:

$-\frac{1}{5}$ $\displaystyle -\frac{1}{5}$

Explanation:

To solve problems where you need to find the slope of a line in a given equation, change the equation so that it matches y-intercept form:

y=mx+b $\displaystyle y=mx+b$

For this equation, first move the 3x over to the other side of the equation.

$\displaystyle 15y + 3x = 4$

-3x $\displaystyle -3x$ -3x $\displaystyle -3x$

The equation should now look like this:

$\displaystyle 15y = -3x + 4$

Then, divide by 15 to isolate the variable $\displaystyle y$.

$\frac{15y}{15} =-\frac{3x}{15} + \frac{4}{15} \rightarrow y =-\frac{3}{15}x + \frac{4}{15}$ $\displaystyle \frac{15y}{15} =-\frac{3x}{15} + \frac{4}{15} \rightarrow y =-\frac{3}{15}x + \frac{4}{15}$

Then simplify

$y =-\frac{3}{15}x + \frac{4}{15} \rightarrow y =-\frac{1}{5}x + \frac{4}{15}$ $\displaystyle y =-\frac{3}{15}x + \frac{4}{15} \rightarrow y =-\frac{1}{5}x + \frac{4}{15}$

Whatever number is before the x in the equation (m) is your slope.

$-\frac{1}{5}$ $\displaystyle -\frac{1}{5}$

Report an Error

Example Question #121 : Equations / Inequalities

Rational_5

Possible Answers:

–2

–1

Correct answer:

Explanation:

Rational_2

Rational_3

Rational_4

Report an Error

Example Question #1 : How To Find The Solution To A Rational Equation With Lcd

Linesmb1

Possible Answers:

–b/(m²– 1)

bm/(m²+ 1)

–bm/(m²+ 1)

b/(m²+ 1)

–b/(m + 1)

Correct answer:

b/(m²+ 1)

Explanation:

Linesmb5

Linesmb4

Report an Error

Example Question #1 : How To Find The Solution To A Rational Equation With Lcd

In the equation below, $\displaystyle m$, $\displaystyle p$, and $\displaystyle k$ are non-zero numbers. What is the value of $\displaystyle m$ in terms of $\displaystyle p$ and $\displaystyle k$?

$\frac{1}{m^3}-\frac{1}{k^2}=\frac{1}{p}$ $\displaystyle \frac{1}{m^3}-\frac{1}{k^2}=\frac{1}{p}$

Possible Answers:

$m=p^{\frac{1}{2}}-k^{\frac{1}{3}}$ $\displaystyle m=p^{\frac{1}{2}}-k^{\frac{1}{3}}$

$m=(\frac{p+k^2}{pk^2})^{\frac{1}{3}}$ $\displaystyle m=(\frac{p+k^2}{pk^2})^{\frac{1}{3}}$

$m=\frac{p^2k^3}{p+k^2}$ $\displaystyle m=\frac{p^2k^3}{p+k^2}$

$m=(\frac{p+k^2}{2})^3$ $\displaystyle m=(\frac{p+k^2}{2})^3$

$m=(\frac{pk^2}{p+k^2})^{\frac{1}{3}}$ $\displaystyle m=(\frac{pk^2}{p+k^2})^{\frac{1}{3}}$

Correct answer:

$m=(\frac{pk^2}{p+k^2})^{\frac{1}{3}}$ $\displaystyle m=(\frac{pk^2}{p+k^2})^{\frac{1}{3}}$

Explanation:

Pkm_7-21-13

Pkm2_7-21-13

Report an Error

View ACT Math Tutors

Tobi
Certified Tutor

Northwestern University, Bachelor of Science, Molecular Biology.

View ACT Math Tutors

Linda
Certified Tutor

Long Island University-C W Post Campus, Bachelors, Art Education.

View ACT Math Tutors

Isaias
Certified Tutor

Instituto Tecnológico de Merida (ITM), Bachelor of Science, Biochemical Engineering. Yucatan Center for Scientific Research (...

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

GMAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Boston, SSAT Courses & Classes in Miami, MCAT Courses & Classes in Seattle, SSAT Courses & Classes in Phoenix, ACT Courses & Classes in Boston, SAT Courses & Classes in Atlanta, Spanish Courses & Classes in Seattle, LSAT Courses & Classes in Denver, GRE Courses & Classes in Phoenix

Popular Test Prep

SSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Los Angeles, GRE Test Prep in Boston, GMAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in San Diego, ISEE Test Prep in Phoenix, LSAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Atlanta, SSAT Test Prep in Los Angeles, SSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : How to find the solution to a rational equation with LCD

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #121 : Linear / Rational / Variable Equations

Example Question #121 : Equations / Inequalities

Example Question #121 : Equations / Inequalities

Example Question #1 : How To Find The Solution To A Rational Equation With Lcd

Example Question #1 : How To Find The Solution To A Rational Equation With Lcd

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: