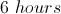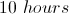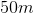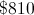Tom paints for a total of \(\displaystyle 4\) hours (2 on his own, 2 with Huck's help). Since he paints at a rate of \(\displaystyle 5\) feet per hour, use the formula

\(\displaystyle distance = rate \times time\) (or \(\displaystyle d = rt\))

to determine the total length of the fence Tom paints.

\(\displaystyle d = (5)(4)\)

\(\displaystyle d = 20\) feet

Subtracting this from the total length of the fence \(\displaystyle 100\) feet gives the length of the fence Tom will NOT paint: \(\displaystyle 100 - 20 = 80\) feet. If Huck finishes the job, he will paint that \(\displaystyle 80\) feet of the fence. Using \(\displaystyle d = rt\), we can determine how long this will take Huck to do:

\(\displaystyle 80 = 8(t)\)

\(\displaystyle t = 10\) hours.

If Huck works \(\displaystyle 10\) hours and Tom works \(\displaystyle 4\) hours, he works \(\displaystyle 6\) more hours than Tom.

This is a FOIL problem. First, we must set up the problem in a form we can use to create the function. To do this we take the opposite sign of each of the numbers and place them in this format: \(\displaystyle (x-5)(x+4)\).

Now we can FOIL.

First: \(\displaystyle x^2\)

Outside: \(\displaystyle 4x\)

Inside: \(\displaystyle -5x\)

Last: \(\displaystyle -20\)

Then add them together to get \(\displaystyle x^{2}+4x-5x-20\).

Combine like terms to find the answer, which is \(\displaystyle x^{2}-x-20=0\).

Set up the equation:

\(\displaystyle \frac{5x + 6x}{2} = 22\)

Solve the equation:

\(\displaystyle 5x + 6x = 44\)

\(\displaystyle 11x = 44\)

\(\displaystyle x=4\)

Find the two numbers:

The two numbers have a ratio of 5:6, therefore the ratio can also be represented as:

\(\displaystyle 5x:6x\)

\(\displaystyle 5(4):6(4)\)

\(\displaystyle 20,24\)

The two numbers are 20 and 24.

Let \(\displaystyle x\) be the number of jelly beans that each friend will receive. She has four friends, so the total number of jelly beans her friends will receive is \(\displaystyle 4x\). Suzanne eats another eight, so the equation can be written as \(\displaystyle 4x+8=60\).

The equation for a line in slope-intercept form is:

\(\displaystyle y=m(x-x_{1})+y_{1}\)

where \(\displaystyle x_{1}\) and \(\displaystyle y_{1}\) are the known coordinates (3,-6).

Substituting gives

\(\displaystyle y=3(x-3)-6\), 

and simplifying gives the final answer:

\(\displaystyle y=3x-15\)

The question asks for a relation between pounds lost and weeks on the diet. If each day your friend cuts 500 calories, the number of pounds he is losing per week is 1:

\(\displaystyle \frac{500 \text{ cal}}{\text{ day}}\cdot \frac{7\text{ days}}{\text{ week}}\cdot \frac{1\text{ pound}}{3500 \text{ cal}}=\frac{1 \text{ pound}}{ \text{ week}}\)

The rate of change, or slope, is therefore -1. The slope is negative because the independent variable (weight in pounds) is decreases as the dependent variable (time in weeks) increases. The y-intercept is 180, because that is how much your friend weighs at the start, when time = 0. Plugging these values into \(\displaystyle y=mx+b\) form, we end up with: 

\(\displaystyle y=-1x+180\)

The distance from the outer edge of the moat to the center of the castle is the radius (100 m) of the larger circle formed by the outer edge of the circular moat.

The radius of the tower's floor (found using the area of the floor), needs to be subracted from 100 m to find the distance fo the bridge. 

\(\displaystyle \sqrt{4900}=70\)

\(\displaystyle 100m - 70m = 30 m\)

The statement, 'The monthly costly to insure your cars varies directly with the number of cars you own' can be mathematically expressed as \(\displaystyle M=kC\). M is the monthly cost, C is the number of cars owned, and k is the constant of variation.

Given that it costs $420 a month to insure 3 cars, we can find the k-value.

\(\displaystyle 420=k * 3\)

Divide both sides by 3.

\(\displaystyle k=140\)

Now, we have the mathematical relationship.

\(\displaystyle M=140C\)

Finding how much it costs to insure 5 cars can be found by substituting 5 for C and solving for M.

\(\displaystyle M=140(5)\)

\(\displaystyle M=700\)

Take every word and translate into math. 

\(\displaystyle 20\) more than means that you need to add \(\displaystyle 20\) to something which is \(\displaystyle x\).

Anytime you see "is" means equal.

Now let's combine and create an expression of \(\displaystyle x+20=40.\)

Take every word and translate into math.

\(\displaystyle 2\) times something means that you need to multiply \(\displaystyle 2\) to something which is \(\displaystyle x\). 

\(\displaystyle 3\) less than means that you need to subtract \(\displaystyle 3\) from \(\displaystyle x\).  

Anytime you see "is" means equal.

Let's combine to get \(\displaystyle 2x=x-3\).