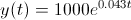We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Applications of antidifferentiation

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Applications Of Antidifferentiation

Find (dy/dx).

sin(xy) = x + cos(y)

Possible Answers:

None of the above

dy/dx = (xcos(xy) + sin(y))/(1 – ycos(xy))

dy/dx = (cos(xy) + sin(y))/(1 – cos(xy))

dy/dx = (1 – cos(xy))/(cos(xy) + sin(y))

dy/dx = (1 – ycos(xy))/(xcos(xy) + sin(y))

Correct answer:

dy/dx = (1 – ycos(xy))/(xcos(xy) + sin(y))

Explanation:

The first step of the problem is to differentiate with respect to (dy/dx):

cos(xy)[(x)(dy/dx) + y(1)] = 1 – sin(y)(dy/dx)

*Note: When differentiating cos(xy) remember to use the product rule. (xy' + x'y)

Step 2: Clean the differentiated problem up

cos(xy)(x)(dy/dx) + cos(xy)y = 1 – sin(y)(dy/dx)

cos(xy)(x)(dy/dx) + sin(y)(dy/dx) = 1 – cos(xy)y

Step 3: Solve for (dy/dx)

dy/dx = (1 – ycos(xy))/(xcos(xy) + sin(y))

Report an Error

Example Question #1 : Solving Separable Differential Equations And Using Them In Modeling

Find the equation of the normal line at (2,0) on the graph $y=x^{3}-6x+4$ .

Possible Answers:

$y'=3x^{2}-6$

$y=\frac{-1}{6}x+\frac{1}{3}$

$y=\frac{-1}{6}x+2$

y=6x-12

y=6x+2

Correct answer:

$y=\frac{-1}{6}x+\frac{1}{3}$

Explanation:

The answer is $y=\frac{-1}{6}x+\frac{1}{3}$ .

$y=x^{3}-6x+4$

$y'=3x^{2}-6$

Now plug in x=2 .

$y'=3(2)^{2}-6 = 6$ now we know 6 is the slope for the tangent line. However, we aren't looking for the slope of the tangent line. The slope of the normal line is the negative reciprocal of the tangent's slope; meaning the slope of the normal is $\frac{-1}{6}$ . Now find the equation of the normal line.

$y-0=\frac{-1}{6}(x-2)$

$y=\frac{-1}{6}x+\frac{1}{3}$

Report an Error

Example Question #2 : Applications Of Antidifferentiation

$f(x) = \frac{x^3}{1-x^2}$

What is the derivative of f(x) ?

Possible Answers:

$\frac{-2x^4-3 x^2(1-x^2)}{(1-x^2)^2}$

$-x$

$\frac{x^2(3-5x^2)}{1-x^2}$

Correct answer:

Explanation:

Use the quotient rule.

${y}' = \frac{(1-x^2)(3x^2)-x^3(-2x)}{(1-x^2)^2} = \frac{x^2(3-3x^2+ 2x^2)}{(1-x^2)^2} = \frac{x^2(3-x^2)}{(1-x^2)^2}$

Report an Error

Example Question #3 : Solving Separable Differential Equations And Using Them In Modeling

Find $y^{'}$ if

$y=\frac{ln(x)}{x^{3}}$

Possible Answers:

$\frac{1+3ln(x)}{x^{4}}$

$\frac{1}{x^{4}}$

$\frac{ln(x)-1}{x^{4}}$

$\frac{3}{x^{3}}$

$y'=\frac{1-3ln(x)}{x^{4}}$

Correct answer:

$y'=\frac{1-3ln(x)}{x^{4}}$

Explanation:

The answer is

$y'=\frac{1-3ln(x)}{x^{4}}$

$y=\frac{ln(x)}{x^{3}}$

$y'=\frac{(\frac{1}{x})x^{3}-ln(x)(3x^{3})}{x^{6}}$

$y'=\frac{x^{2}(1-3ln(x))}{x^{6}}$

$y'=\frac{1-3ln(x)}{x^{4}}$

Report an Error

Example Question #3 : Applications Of Antidifferentiation

Find the derivative:

f(x)=x^3-3x^2

Possible Answers:

f'(x)=3x^2-6x

f'(x)=3x-6

f'(x)=x^2-6x

f'(x)=3x^3-6x^2

Correct answer:

f'(x)=3x^2-6x

Explanation:

To find the derivative, multiply the exponent by the coefficent in front of the x term and then decrease the exponent by 1:

f'(x)=3x^2-6x

Report an Error

Example Question #6 : Solving Separable Differential Equations And Using Them In Modeling

Find the solution to the equation $y'=y$ at $x=2$ with initial condition $y(0)=2$ .

Possible Answers:

$2e^2$

$1$

$e$

$2e$

$e^2$

Correct answer:

$2e^2$

Explanation:

First, we need to solve the differential equation of $y'=y$ .

y'=y

$\frac{dy}{dx}=y$

$\frac{dy}{y}=dx$

$\int \frac{dy}{y}=\int dx$

ln(y)=x+c , where is a constant

y=e^xe^c

y=Ce^x , where is a constant

To find , use the initial condition, y(0)=2 , and solve:

C=2

Therefore, $y=2e^x$ .

Finally, at x=2 , $y(2)=2e^2$ .

Report an Error

Example Question #27 : Integrals

Solve the differential equation: $\frac{dy}{dx}=-2xy$

Note that (-1,2) is on the curve.

Possible Answers:

y=-2

y=-x^2+ln(2)+1

y=ln(2)+1

$y=2e^{1-x^2}$

Correct answer:

$y=2e^{1-x^2}$

Explanation:

In order to solve differential equations, you must separate the variables first.

$\frac{dy}{y}=-2xdx$

$\int \frac{dy}{y}= \int -2xdx$

ln(y)=-x^2+C

Since point (-1,2) is on the curve, ln(2)=-1+C .

ln(2)+1=C

ln(y)=-x^2+ln(2)+1

To get rid of the log, raise every term to the power of e:

$e^{ln(y)}=e^{-x^2}*e^{ln(2)}*e^1$

$y=2e^{1-x^2}$

Report an Error

Example Question #6 : Applications Of Antidifferentiation

Suppose $1000 is invested in an account that pays 4.3% interest compounded continuously. Find an expression for the amount in the account after time .

Possible Answers:

$y(t)=1000e^{0.043t}$

$y(t)=1000e^{t}$

$y(t)=4.3e^{1000t}$

$y(t)=4.3e^{t}$

$y(t)=43e^{1000t}$

Correct answer:

$y(t)=1000e^{0.043t}$

Explanation:

The differential equation is $\frac{dy}{dt}=0.043y$ , with boundary condition $y(0)=1000$ .

This is a separable first order differential equation.

$\frac{1}{y}dy=0.043dt$

Integrate both sides.

$ln(y)=0.043t+c$

$e^{ln(y)}=e^{0.043t+c}$

$y=Ce^{0.043t}$

Plug in the initial condition above to see that C=1000 .

Report an Error

Example Question #8 : Solving Separable Differential Equations And Using Them In Modeling

Find the solution to the differential equation

$\frac{dy}{dx} = \frac{x^{2}+ 4x}{y^{2}}$ when f(0) = 3 .

Possible Answers:

$\frac{y^{3}}{3} = \frac{x^{3}}{3} + 2x^{2}$

$y^{3} = x^{3} + 2x^{2} + 9$

$\frac{y^{3}}{3} = \frac{x^{3}}{3} + 2x^{2} - 27$

$\frac{1}{y} = \frac{1}{x} + 2x^{2} + 9$

$\frac{y^{3}}{3} = \frac{x^{3}}{3} + 2x^{2} + 9$

Correct answer:

$\frac{y^{3}}{3} = \frac{x^{3}}{3} + 2x^{2} + 9$

Explanation:

First, separate the variables of the original differential equation:

$\frac{dy}{dx} = \frac{x^{2}+ 4x}{y^{2}} \Rightarrow y^{2}dy = (x^{2} + 4x)dx$ .

Then, take the antiderivative of both sides, which gives

$\frac{y^{3}}{3} = \frac{x^{3}}{3} + 2x^{2} + C$ .

Use the given condition f(0) = 3 , plugging in

x = 0 and y=3 , to solve for . This gives c=9 , so the correct answer is

$\frac{y^{3}}{3} = \frac{x^{3}}{3} + 2x^{2} + 9$ .

Report an Error

Example Question #31 : Integrals

Differentiate y=3x^3+5x+7 .

Possible Answers:

y' = 9x^2+5

y'=9x^3+5x

y'=9x^2+5x+x

y'=6x^2+5

Correct answer:

y' = 9x^2+5

Explanation:

While differentiating, multiply the exponent with the coefficient then subtract the exponent by one.

$y'=(3\cdot3)x^{3-1}+(5\cdot1)x^{1-1}+(7\cdot0)$

y'=9x^2+5

Report an Error

View AP Calculus AB Tutors

Yucheng
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mechanical Engineering.

View AP Calculus AB Tutors

Mohammad
Certified Tutor

Rutgers University-New Brunswick, Bachelor of Science, Mathematics. Rutgers University-New Brunswick, Master of Science, Stat...

View AP Calculus AB Tutors

James
Certified Tutor

University of Georgia, Bachelor in Arts, Political Science and Government.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in San Diego, Spanish Tutors in San Francisco-Bay Area, Statistics Tutors in Chicago, ISEE Tutors in Atlanta, Reading Tutors in Washington DC, French Tutors in Dallas Fort Worth, Math Tutors in Houston, Physics Tutors in Philadelphia, English Tutors in Denver, Reading Tutors in San Francisco-Bay Area

Popular Courses & Classes

LSAT Courses & Classes in New York City, SAT Courses & Classes in Miami, GMAT Courses & Classes in Miami, GMAT Courses & Classes in Washington DC, GMAT Courses & Classes in Seattle, GRE Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Seattle, GMAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Seattle, Spanish Courses & Classes in Denver

Popular Test Prep

GMAT Test Prep in Washington DC, SAT Test Prep in Philadelphia, ISEE Test Prep in Dallas Fort Worth, GRE Test Prep in Miami, LSAT Test Prep in Miami, ACT Test Prep in Miami, GMAT Test Prep in Boston, GMAT Test Prep in Seattle, GMAT Test Prep in Philadelphia, ISEE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Applications of antidifferentiation

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #1 : Applications Of Antidifferentiation

Example Question #1 : Solving Separable Differential Equations And Using Them In Modeling

Example Question #2 : Applications Of Antidifferentiation

Example Question #3 : Solving Separable Differential Equations And Using Them In Modeling

Example Question #3 : Applications Of Antidifferentiation

Example Question #6 : Solving Separable Differential Equations And Using Them In Modeling

Example Question #27 : Integrals

Example Question #6 : Applications Of Antidifferentiation

Example Question #8 : Solving Separable Differential Equations And Using Them In Modeling

Example Question #31 : Integrals

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: