All AP Calculus AB Resources
Example Questions
Example Question #1 : Techniques Of Antidifferentiation
A projectile is shot up from a platform 




Separate velocity variables and solve.
Plug in intial conditions
Example Question #1 : Integrals
A gun sends a bullet straight up with a launch velocity of 220 ft/s. It reaches a height of 

The bullet will be at a height of 500 ft on the way up and on the way down.
We use the position equation 


We then plug that into the velocity equation, which is the derivative of the position function. 
We can see that plugging in the value of 



Example Question #1 : Techniques Of Antidifferentiation
The position of a particle as a function of time is given below:
At what values of 
In order to find the point at which the particle changes direction, we must determine whenever the velocity of the particle changes sign (from positive to negative, or from negative to positive).
We will need to have the function of the particle's velocity before we can determine where the velocity changes sign. Because the velocity is the derivative of position with respect to time, we can write the function for velocity, 
If we set 
The possible points where 

First, we can try a value less than 2, such as 1, and then a value between 2 and 4, such as 3. We will evaluate 


Thus, 

Lastly, we will evaluate the velocity at a value of 
The sign of the velocity has switched back to positive, so the particle does indeed change direction at 
The answer is 

Example Question #2 : Techniques Of Antidifferentiation
The speed of a car traveling on the highway is given by the following function of time:
Note that
What does this mean?
The car is not decelerating at time 
The car is not moving at time 
The car takes 
The car is not accelerating at time 
The car's speed is constantly changing at time 
The car is not moving at time 
The function 






Example Question #1 : Techniques Of Antidifferentiation
A jogger leaves City 
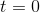
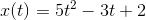
where 
Find the velocity of the jogger at 15 minutes.
To find velocity, one has to use the first derivative of 


Note the units have to be ft/min.
Example Question #3 : Techniques Of Antidifferentiation
Consider the function
Find the minimum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90588/gif.latex)
To find potential minima of the function, take the first derivative of 
Set the derivative to 0:
We solve for 

We can double check that 
which means the function is concave up, so that the point we found is a minimum.
Example Question #4 : Techniques Of Antidifferentiation
Find the x coordinate of the minimum of 
![\left [ -2, 2\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106125/gif.latex)
First, find the derivative, which is:
Set that equal to 0 to find your critical points:
Evaluate f at each critical point and endpoint over [-2, 2]:
The least of those numbers is the minimum. Because f(-2)=-32, that is the minimum.
Example Question #1 : Antiderivatives Following Directly From Derivatives Of Basic Functions
What is the local minimum of 

The y-value is constant throughout that range.
There is no local minimum in that range.
To find the maximum, we need to look at the first derivative.
To find the first derivative, we can use the power rule. To do that, we lower the exponent on the variables by one and multiply by the original exponent.
We're going to treat 

Notice that 
When looking at the first derivative, remember that if the output of this equation is positive, the original function is increasing. If the derivative is negative, then the function is decreasing.
Because we want the MINIMUM, we want to see where the derivative changes from negative to positive.
Notice that 


Example Question #1 : Techniques Of Antidifferentiation
Integrate,


Integrate
1) Apply the sum rule for integration,
2) Integrate each individual term and include a constant of integration,
Further Discussion
Since indefinite integration is essentially a reverse process of differentiation, check your result by computing its' derivative.
This is the same function we integrated, which confirms our result. Also, because the derivative of a constant is always zero, we must include "C" in our result since any constant added to any function will produce the same derivative.
Example Question #5 : Techniques Of Antidifferentiation
Certified Tutor
Certified Tutor
All AP Calculus AB Resources


















![v(t)=x'(t)=\frac{d}{dx}[\frac{t^{3}}{3}-3t^{2}+8t]=\frac{3t^{2}}{3}-6t+8=t^{2}-6t+8](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/24744/gif.latex)









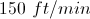







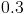
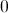
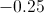





















![\int[x^2 +\sin(x)-3]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/749356/gif.latex)




![\int[x^2 +\sin(x)-3]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/749357/gif.latex)








![\begin{align*}&\text{In performing an integral, familiarity with derivative rules}\\&\text{can prove useful. After all, an integral is essentially the}\\&\text{opposite operation of a derivative. Consider how in a derivative}\\&\text{we’d use the chain rule to multiply the derivative of the “inside”}\\&\text{of a function by the derivative of the outside? Integrals, in}\\&\text{similar fashion, entail a division.}\\&\text{Utilizing integral rules:}\\&\int[cos(ax)]=\frac{sin(ax)}{a}\\&\int_{8}^{11.5}(\frac{(27cos(x + 1))}{8})dx=\frac{(27sin(x + 1))}{8}|_{8}^{11.5}\\&\text{Now we just subtract the function value at the lower bound from that of the upper bound:}\\&\int_{8}^{11.5}(\frac{(27cos(x + 1))}{8})dx=\frac{(27sin((11.5) + 1))}{8}-(\frac{(27sin((8) + 1))}{8})\\&\int_{8}^{11.5}(\frac{(27cos(x + 1))}{8})dx=-1.61\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/931547/gif.latex)



