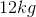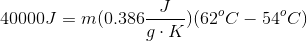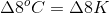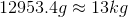AP Physics B : Understanding Heat and Temperature
Study concepts, example questions & explanations for AP Physics B
All AP Physics B Resources
Example Questions
Example Question #2 : Ap Physics 2
Which of the following is not an acceptable unit for specific heat?
Specific heat is most commonly applied in the equation to determine the heat required/released during a temperature change:
Rearranging this equal, we can see that this units of specific heat are units of heat per units of mass times units of temperature.
Heat energy can have the units of Joules or calories. Mass can have units of grams or kilograms. Temperature can have units of Kelvin, degrees Celsius, or degrees Fahrenheit. British thermal units (Btu) is a less common unit of heat, defined by the amount of heat required to raise one pound of water by one degree Fahrenheit.
Newtons are a unit of force, and cannot be used in the units for specific heat.
Example Question #1 : Ap Physics 2
A sample of copper is heated with 
Our equation for temperature change using specific heat is:
Since Celsius and Kelvin use the same interval scale, we do not need to convert to find the change in temperature. Using the initial and final temperatures, the energy input, and the specific heat of copper, we can calculate the mass of copper present.
To simplify, we will solve for the temperature change separately.
Since the scale for Celsius and Kelvin is the same, this change is the same in either scale.
Use this value back in the original calculation.
Convert to kilograms to simplify.
All AP Physics B Resources
