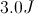All AP Physics C Electricity Resources
Example Questions
Example Question #121 : Ap Physics C
A 0.8kg ball is dropped from rest from a cliff that is 150m high. Use conservation of energy to find the vertical velocity of the ball right before it hits the bottom of the cliff.
The conservation of energy equation is 
The ball starts from rest so . It starts at a height of 150m, so
. When the ball reaches the bottom, height is zero and thus,
and
. The conservation of energy equation can be adjusted below.
Solve for v.
Example Question #1 : Work, Energy, And Power
Starting from rest, a skateboarder travels down a 25o incline that's 22m long. Using conservation of energy, calculate the skateboarder's speed when he reaches the bottom. Ignore friction.
Conservation of energy states that 
The skateboarder starts from rest; thus, and
. At the bottom of the incline,
and
.
Solve for v.
Using trigonometry, .
Example Question #1 : Energy
A 


Relevant equations:
Determine initial kinetic and potential energies when the ball is dropped.
Determine final kinetic and potential energies, when the ball has fallen to 
Use conservation of energy to equate initial and final energy sums.
Solve for the final velocity.
Example Question #2 : Energy
A solid metal object with mass of 


This is a conservation of energy problem. First we have to find the work done by gravity. This can be found using:
It is given to us that the work done by the drag force is 

Since this is a conservation of energy problem, we set the net work equal to the kinetic energy equation:


Example Question #1 : Energy
If a roller coaster car is traveling at 


This is a classic conservation of energy problem. We know that potential energy and kinetic energy both have to conserve. So we use the following equation:
What this equations says is, the sum of kinetic and potential energy is same at varying heights and velocities.
We can simplify this equation by cancelling out all the m terms.
We know all the terms except for 






If we plug in all the numbers and solve for 

Example Question #1 : Kinetic Energy
A train car with a mass of 2400 kg starts from rest at the top of a 150 meter-high hill. What will its velocity be when it reaches the bottom of the hill, assuming that the bottom of the hill is the reference level.
The law of conservation of energy states:
If the car starts at rest, then the initial kinetic energy = 0 J.
If the car ends at the reference height, the final potential energy = 0 J.
Subsituting these values, the equation becomes:
The initial potential energy can be determined by:
The final kinetic energy equation is:
Substituting the initial potential energy and final kinetic energy into our modified conservation of energy equation, we get:
Example Question #1 : Kinetic Energy
An object has a mass of 5kg and has a position described by the given function:
What is the object's kinetic energy after two seconds?
Kinetic energy is defined by the equation:
Taking the derivative of the position function allows us to obtain the velocity function:
We can now determine the velocity after two seconds:
Now that we know our velocity, we can solve for the kinetic energy.
Example Question #2 : Kinetic Energy
An object starts from rest and accelerates at a rate of 
Kinetic energy is given by the equation:
We can find the velocity using the given acceleration and time:
Use this velocity to find the kinetic energy after three seconds:
Example Question #3 : Kinetic Energy
A 120kg box has a kinetic energy of 2300J. What is its velocity?
The formula for kinetic energy of an object is:
The problem gives us the mass and the kinetic energy, and asks for the velocity, so we can rearrange the equation:
Use our given values for kinetic energy and mass to solve:
Example Question #231 : Ap Physics C
Calculate how much potential energy a vertical standing spring gains if someone puts a 4kg box on top of it. Take the spring constant to be 120N/s.
First, find out how much the spring compresses when the 4kg box is put on top of it. To find this, consider what forces are acting on the box when it is resting on the spring. The forces acting on it are the upward spring force, , and the downward gravitational force,
; thus, the net force acting on the box is given by the equation below.
We have chosen the upward direction to be positive and the downward direction to be negative. The net force is equal to zero because the box is at rest. Solve for x.
Then use this value to find the potential energy of the spring.
So when the box is placed on top of the spring, the spring gains a potential energy of 6.5J.
Certified Tutor
All AP Physics C Electricity Resources