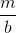Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 1 : Constant of Proportionality

Study concepts, example questions & explanations for Calculus 1

Create An Account

All Calculus 1 Resources

10 Diagnostic Tests 438 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #161 : Classifying Algebraic Functions

Suppose a blood cell increases proportionally to the present amount. If there were blood cells to begin with, and blood cells are present after hours, what is the growth constant?

Possible Answers:

$\frac{3}{2}$

$\frac{1}{2}ln\left(\frac{3}{2}\right)$

$ln\left(\frac{3}{2}\right)$

$ln\left(\frac{2}{3}\right)$

$\frac{2}{3}$

Correct answer:

$\frac{1}{2}ln\left(\frac{3}{2}\right)$

Explanation:

The population size P(t) after some time is given by:

P(t)= P_ie^k^t

where P_i is the initial population.

At the start, there were 30 blood cells.

P_i=P(0)=30

Substitute this value into the given formula.

P(t)= 30e^k^t

After 2 hours, 45 blood cells were present. Write this in mathematical form.

P(2)=45

Substitute this into P(t)= 30e^k^t , and solve for .

45= 30e^k^(^2^)

$\frac{3}{2}= e^2^k$

$ln\left(\frac{3}{2}\right)=ln(e^2^k)$

$2k=ln\left(\frac{3}{2}\right)$

$k=\frac{1}{2}ln\left(\frac{3}{2}\right)$

Report an Error

Example Question #1 : Constant Of Proportionality

Given any linear function y=mx+b , determine the direct constant of proportionality

Possible Answers:

m/b

$\frac{m}{b}$

$\frac{m-b}{m}$

Correct answer:

Explanation:

Direct constant of proportionality for any given function y, between any x values, is given by

$r=\frac{\Delta y}{\Delta x}$ , where is the direction constant of proportionality

In the case of a linear function

$\frac{\Delta y}{\Delta x}$ is the same thing as the slope.

Therefore, the constant of proportionality is

Report an Error

Example Question #2 : Constant Of Proportionality

Find the direct constant of proportionality of x^2 from to 2.5 .

Possible Answers:

3.5

2.5

Correct answer:

3.5

Explanation:

To determine the direct constant of proportionality, we determine the rate of change from x=1 and x=2.5 for x^2 .

Rate of change is determined by

$r=\frac{\Delta y}{\Delta x}$ .

In our case, y=x^2 between x=1 and x=2.5 , the rate of change is

$r=\frac{2.5^2-1}{2.5-1}=\frac{5.25}{1.5}=3.5$ .

Report an Error

Example Question #1 : Constant Of Proportionality

Find the direct constant of proportionality of y=ln(3x) from x=2 to x=4 .

Possible Answers:

$r= \frac{ln(2)}{2}$

r= ln(12)-ln(6)

$r= \frac{6}{2ln(2)}$

$r= \frac{2}{ln(2)}$

Correct answer:

$r= \frac{ln(2)}{2}$

Explanation:

Direct constant of proportionality is given by

$r=\frac{\Delta y}{\Delta x}$ .

Since y=ln(3x) and $\Delta x= 4-2=2$

$r= \frac{\Delta y}{\Delta x}=\frac{ln(3*4)-ln(3*2)}{2}= \frac{ln(2)}{2}$

Report an Error

Example Question #162 : Classifying Algebraic Functions

Suppose a population of bacteria increases from 100 to 1000 in $30\: min$ . What is the constant of growth?

Possible Answers:

$\frac{\ln(10)}{30}$

$e^{30}$

None of these

$\ln(10)$

Correct answer:

$\frac{\ln(10)}{30}$

Explanation:

The equation for population growth is given by $P=Ae^{kt}$ . is the population, is the intial value, is time, and is the growth constant. We can plug in the values we know at time t=0 and solve for .

$100=Ae^{0k}=A$

Now that we solved for , we can plug in what we know for time t=30 and solve for .

$1000=100e^{30k}$

$e^{30k}=10$

$30k=\ln(10)$

$k=\frac{\ln(10)}{30}$

Report an Error

Example Question #161 : Classifying Algebraic Functions

A population of deer grew from 50 to 200 in 7 years. What is the growth constant for this population?

Possible Answers:

None of these

$\ln(4)$

$\frac{4}{7}$

$\frac{\ln(4)}{7}$

$\ln(7)$

Correct answer:

$\frac{\ln(4)}{7}$

Explanation:

The equation for population growth is given by $P=Ae^{kt}$ . P is the population, is the intial value, is time, and is the growth constant. We can plug in the values we know at time t=0 and solve for .

$50=Ae^{0k}=A$

Now that we have solved for we can solve for at t=7

$200=50e^{7k}$

$e^{7k}=4$

$7k=\ln(4)$

$k=\frac{\ln(4)}{7}$

Report an Error

Example Question #4 : How To Find Constant Of Proportionality Of Rate

A population of mice has 200 mice. After 6 weeks, there are 1600 mice in the population. What is the constant of growth?

Possible Answers:

$\frac{\ln(8)}{6}$

$\ln(8)$

$\frac{\ln(6)}{6}$

$\frac{\ln(6)}{8}$

Correct answer:

$\frac{\ln(8)}{6}$

Explanation:

The equation for population growth is given by $P=Ae^{kt}$ . is the population, is the intial value, is time, and is the growth constant. We can plug in the values we know at time t=0 and solve for .

$200=Ae^{0k}=A$

Now that we have we can solve for at t=6 .

$1600=200e^{6k}$

$e^{6k}=8$

$6k=\ln(8)$

$k=\frac{\ln(8)}{6}$

Report an Error

Example Question #4 : Constant Of Proportionality

Find the direct constant of proportionality of y=3sec(x) from x=0 to $x=\frac{\pi}{3}$ .

Possible Answers:

$k=\frac{9}{\pi}$

$k=-\frac{\pi}{9}$

$k=\frac{\pi}{9}$

is undefined

Correct answer:

$k=\frac{9}{\pi}$

Explanation:

Direct constant of proportionality is given by

$k=\frac{\Delta y}{\Delta x}$ , where $\Delta y$ is the change in the position and $\Delta x$ is the change in the position.

Since y=3sec(x) , and we're going from x=0 to $x=\frac{\pi}{3}$

$\Delta y=3sec(\frac{\pi}{3})-3sec(0)=6-3=3$

$\Delta x=\frac{\pi}{3}-0=\frac{\pi}{3}$

$k=\frac{3}{\frac{\pi}{3}}=\frac{9}{\pi}$

Report an Error

Example Question #161 : Classifying Algebraic Functions

The rate of decrease of the dwindling wolf population of Zion National Park is proportional to the population. The population decreased by 7 percent between 2009 and 2011. What is the constant of proportionality?

Possible Answers:

-0.011

0.130

-0.044

-0.009

-0.036

Correct answer:

-0.036

Explanation:

We're told that the rate of growth of the population is proportional to the population itself, meaning that this problem deals with exponential growth/decay. The population can be modeled thusly:

$p(t)=p_0e^{kt}$

Where p_0 is an initial population value, and is the constant of proportionality.

Since the population decreased by 7 percent between 2009 and 2011, we can solve for this constant of proportionality:

$(1-0.07)y_0=y_0e^{k(2011-2009)}$

$0.93=e^{2k}$

2k=ln(0.93)

$k=\frac{ln(0.93)}{2}=-0.036$

Report an Error

Example Question #1 : Exponential Growth Applications

The rate of growth of the Martian Transgalactic Constituency is proportional to the population. The population increased by 23 percent between 2530 and 2534 AD. What is the constant of proportionality?

Possible Answers:

0.07

0.05

0.12

-0.37

1.04

Correct answer:

0.05

Explanation:

We're told that the rate of growth of the population is proportional to the population itself, meaning that this problem deals with exponential growth/decay. The population can be modeled thusly:

$p(t)=p_0e^{kt}$

Where p_0 is an initial population value, and is the constant of proportionality.

Since the population increased by 23 percent between 2530 and 2534 AD, we can solve for this constant of proportionality:

$(1+0.23)y_0=y_0e^{k(2534-2530)}$

$1.23=e^{4k}$

4k=ln(1.23)

$k=\frac{ln(1.23)}{4}=0.05$

Report an Error

View Calculus Tutors

Yuliya
Certified Tutor

University of Maryland-College Park, Bachelor of Science, Mathematics. George Washington University, Masters in Education, Ed...

View Calculus Tutors

Andrew
Certified Tutor

University of Wisconsin-Stevens Point, Bachelor of Science, Mathematics. University of Wisconsin-Oshkosh, Master of Science, ...

View Calculus Tutors

Abhisek
Certified Tutor

University of Florida, Bachelor of Engineering, Computer Science.

All Calculus 1 Resources

10 Diagnostic Tests 438 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Seattle, LSAT Tutors in Boston, Algebra Tutors in Seattle, Reading Tutors in Houston, MCAT Tutors in New York City, Calculus Tutors in San Diego, Algebra Tutors in Denver, LSAT Tutors in Seattle, Statistics Tutors in Dallas Fort Worth, Math Tutors in Dallas Fort Worth

Popular Courses & Classes

LSAT Courses & Classes in Atlanta, SSAT Courses & Classes in New York City, ISEE Courses & Classes in Atlanta, Spanish Courses & Classes in Houston, SSAT Courses & Classes in Phoenix, GRE Courses & Classes in Chicago, SSAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Atlanta, ACT Courses & Classes in Phoenix, GMAT Courses & Classes in Miami

Popular Test Prep

SSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in San Diego, GMAT Test Prep in Miami, GMAT Test Prep in Boston, SAT Test Prep in Seattle, ISEE Test Prep in Washington DC, SSAT Test Prep in Los Angeles, ACT Test Prep in Chicago, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 1 : Constant of Proportionality

Study concepts, example questions & explanations for Calculus 1

All Calculus 1 Resources

Example Questions

Example Question #161 : Classifying Algebraic Functions

Example Question #1 : Constant Of Proportionality

Example Question #2 : Constant Of Proportionality

Example Question #1 : Constant Of Proportionality

Example Question #162 : Classifying Algebraic Functions

Example Question #161 : Classifying Algebraic Functions

Example Question #4 : How To Find Constant Of Proportionality Of Rate

Example Question #4 : Constant Of Proportionality

Example Question #161 : Classifying Algebraic Functions

Example Question #1 : Exponential Growth Applications

All Calculus 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: