All College Algebra Resources
Example Questions
Example Question #21 : College Algebra
Solve for 
The first thing we notice about this problem is that 
The question is, which base should we choose for the log? We should use the natural log (log base e) because the right-hand side of the equation already has e as a base of an exponent. As you will see, things cancel out more nicely this way.
Take the natural log of both sides:
Rewrite the right-hand side of the equation using the product rule for logs:
Now rewrite the whole equation after bringing down those exponents.


Now we just divide by 

Example Question #22 : College Algebra
Solve 
The original equation is:
Subtract 
Divde both sides by 
Take the natural logarithm of both sides:
Divde both sides by 
Example Question #23 : College Algebra
Solve for 

If necessary, round to the nearest tenth.
No solution
Give both sides the same base, using e:

Because e and ln cancel each other out, 
Solve for x and round to the nearest tenth:
Example Question #24 : College Algebra
Solve the following for x:
To solve this exponential function, you must first "undo" the e by taking the natural log of both sides. Thus,
Then, to isolate x, you must subtract two from both sides. Thus,
Example Question #25 : College Algebra
Solve the following for x:
To solve, you must isolate x. The first two steps are to divide both sides by 2 and then take the natural log of both sides.
Finally, you must divide both sides by 4.
Example Question #22 : College Algebra
Give the solution set for the exponential equation shown below for the following cases:
Case 1,
Case 2
Case 1:
Case 2:
There is not enough information to find 

Case 1:
All real values of 
Case 2:
Case 1:
There are no solutions,
Case 2:
Case 1:
All real values of 
Case 2:
All real values of 
Case 1:
Case 2:
Case 1:
All real values of 
Case 2:
Case 1,
This is true for all real values of 
Case 2
Take the natural logarithm of both sides (note that we could use any logarithm but it's convenient to just choose the natural logarithm).
Use the rule for pulling out exponents 
Note that if you were to divide out by 



Expand with the distributive property,
Collect and isolate terms with 
Factor out 


What's remarkable about this solution is that it was obtained without specifying any value for 


Example Question #23 : College Algebra
Solve for 
Solve for 
Note the rules for logarithms,



There is more than one way to get started, but notice that if we divide out by 
Take the natural log of both sides,
Use rule (3) to pull out the exponents,
Expand with the distributive property,
Collect terms with 

Divide out to solve for 

The numerator can be simplified using rules (2) and (3). Use rule (3) on the 
So now the numerator can be written,
Bringing back the denominator in equation (4) gives,

Example Question #2 : Solving Exponential Functions
Solve this equation:
To solve 
Example Question #26 : College Algebra
Find the value of a:
For this problem, we can use the fact that the exponent and logarithm are inverses of each other. So if we raise both sides up as exponents:
The left side of the equation cancels and we get that
Example Question #31 : Exponential And Logarithmic Functions
Solve for 
To more easily solve for x, we need to try to express the right hand side of the equation in terms of a number of base 4. 256 is simply 
Rewriting the equation with this discovery yields
Since both bases are the same, we can set the exponents equal to each other and solve for x.
Certified Tutor
All College Algebra Resources
























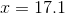




































![\ln\left(a^{10x-1} \right ) = \ln\left[b^{10x-1}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/736239/gif.latex)



![10x[\ln(a)-\ln(b)]=\ln(a)-\ln(b)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/736247/gif.latex)














![y[\ln(5)-ln(7)]=-ln(5)-ln(7)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/736200/gif.latex)
































