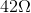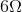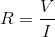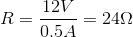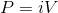This question requires no math to correctly answer! You should not need to 'brute force' it. Although it is designed to appear time consuming, it should be relatively easily once the principle of resistors in parallel is understood. Whenever two resistors are connected in parallel, the net resistance must be less than the resistance of either of the two alone. When resistors are connected in series, the net resistance must be more than the resistance of either alone.

Explanation of correct answer:

\(\displaystyle R1\) and \(\displaystyle R2\) in parallel, connected to \(\displaystyle R3\) in series - It is possible to 'eyeball' this to see that this is at least feasible. \(\displaystyle R1\) and \(\displaystyle R2\) in parallel must make a network with an overall resistance less than \(\displaystyle 50\Omega\). When added in series with \(\displaystyle R3\) (\(\displaystyle 10\Omega\)), the overall may fall between \(\displaystyle 40\Omega\) and \(\displaystyle 45\Omega\). To confirm, one could do the math to calculate the overall resistance, but the point of this question is to use general principles to quickly eliminate the other, incorrect answer choices.

Explanations of incorrect answers:

\(\displaystyle R1\), \(\displaystyle R2\), and \(\displaystyle R3\) in parallel - This combination cannot possibly work since the overall resistance must be less than \(\displaystyle 10\Omega\) (the smallest resistor in parallel).

\(\displaystyle R2\) and \(\displaystyle R3\) in parallel, connected to \(\displaystyle R1\) in series - Regardless of the overall resistance of \(\displaystyle R2\) and \(\displaystyle R3\) in parallel, the connection with \(\displaystyle R1\) in series makes the total resistance more than \(\displaystyle 100\Omega\).

\(\displaystyle R1\) and \(\displaystyle R3\) in parallel; \(\displaystyle R2\) is not necessary - Placing \(\displaystyle R1\) and \(\displaystyle R3\) in parallel must result in a resistance less than \(\displaystyle 10\Omega\).

\(\displaystyle R1\), \(\displaystyle R2\), and \(\displaystyle R3\) in series - Connecting resistors in series results in an overall resistance greater than that of any one alone. Since \(\displaystyle R1\) and \(\displaystyle R2\) are included in series, the sum of the resistances is obviously much greater than what we are asked to produce and this choice can be immediately eliminated.

In this question, we're given a number of parameters of a circuit and are asked to find how we can use these various parameters to show the capacitance of the circuit's capacitor.

First, recall what a capacitor is; something that stores charge for a given voltage difference. In other words, when there is a voltage difference between the two plates of a capacitor, a certain amount of charge can be stored on these plates. The more charge that can be stored for a given voltage difference, the greater that capacitor's capacitance. This can be shown by the following equation.

\(\displaystyle C=\frac{Q}{V}\)

From the above expression, \(\displaystyle C\) is the capacitance which we are trying to find a proper expression for. \(\displaystyle Q\) is the charge accumulated on the plates, which is one parameter we're given. Voltage, \(\displaystyle V\), on the other hand, is not provided.

To put the voltage into different terms, we'll need to use Ohm's law, which states the following.

\(\displaystyle V=iR\)

In other words, the voltage is proportional to both the current and the resistance of the circuit.

Since we are given both current and resistance as known parameters in the question stem, we can use these for our final answer. By substituting the \(\displaystyle V\) in the capacitance expression with \(\displaystyle iR\), we obtain the following answer.

\(\displaystyle C=\frac{Q}{iR}\)

The capacitance of a parallel plate capacitor is proportional to the inverse of the distance between the plates. If the distance is halved, the capacitance is doubled.

The formula for finding the voltage of a simple RC circuit is 

\(\displaystyle V_{c} = V_{s} (1-e^{(\frac{-t}{RC})})\), where \(\displaystyle V_c\) is the capacitor voltage, \(\displaystyle V_s\) is the source voltage, \(\displaystyle R\) is the resistance, and \(\displaystyle C\) is the capacitance.

We want to know when the capacitor will reach the voltage of the power source \(\displaystyle (V_c = V_s)\) so 

\(\displaystyle 1 = 1 - e^{(\frac{-t}{RC})}\) and thus \(\displaystyle 0 = e^{(\frac{-t}{RC})}\)

Using the properties of natural logs yields

\(\displaystyle 1 = \frac{-t}{RC} = \frac{-t}{10000*(6\times 10^{-3})}\)

Solving for \(\displaystyle t\) yields \(\displaystyle t=-60=60s\)

We are asked to calculate the power dissipated through a resistor connected to a battery. We know that \(\displaystyle P=\frac{V^2}{R}\). Substituting the values given above, \(\displaystyle 60W=\frac{(24V)^2}{R}\). Solving for R yields \(\displaystyle 9.6\Omega\).

This question requires two steps: the first is to calculate the peak voltage of the AC current, and the second requires conversion of the peak voltage to an RMS voltage. We are told that the current is \(\displaystyle 100V\) peak-to-peak. Thus, the peak voltage is half of this, or \(\displaystyle 50V\). By definition, to convert peak voltage to RMS voltage, we must divide the peak voltage by \(\displaystyle \sqrt{2}\):

\(\displaystyle \frac{50V}{\sqrt{2}} = 35.5V\)

The power dissipated in each light bulb is \(\displaystyle \frac{V^2}{R}\). Since there are two light bulbs, the total power dissipated is \(\displaystyle 2\frac{V^2}{R}=2\frac{(12~\text{V})^2}{100~\Omega}\)

Ohm's law is \(\displaystyle V=IR\).

In this case, \(\displaystyle V=12V\) and \(\displaystyle I=0.5A\).

 Solving for the resistance, \(\displaystyle R\), we get:

\(\displaystyle R=\frac{V}{I}\)

Substitute known values and solve for the unknown resistance:

\(\displaystyle R=\frac{12V}{0.5A}=24\Omega\)

Ohm's law relates voltage to current and resistance, \(\displaystyle V = IR\). To find the current, we simply divide the voltage by the resistance and get \(\displaystyle \frac{9\text{V}}{10\Omega} = 0.9A\)

For this problem, let's first take note of what we know and what we don't. We're given voltage and power, but we're not given resistance or current. Since we have two unknowns, we're going to need two equations.

One of the equations that we can use is the power generated by current flowing through a resistor.

\(\displaystyle P=iV\)

In addition, we also need to use Ohm's law.

\(\displaystyle V=iR\)

With these two equations in mind, we can relate them to one another by isolating the variable for current in one equation and then substituting it into the other one.

Manipulating Ohm's law:

\(\displaystyle i=\frac{V}{R}\)

Then substituting this into the power equation:

\(\displaystyle P=\frac{V^{2}}{R}\)

And rearranging to isolate the variable for resistance:

\(\displaystyle R=\frac{V^{2}}{P}\)

Now we just need to plug in the values from the question stem to obtain the answer:

\(\displaystyle R=\frac{(6\:V)^{2}}{30\:W}=\frac{36\:V^{2}}{30\:W}=1.2\:\Omega\)