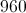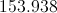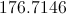We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 7th Grade Math : Area of a circle

Study concepts, example questions & explanations for Common Core: 7th Grade Math

Create An Account

All Common Core: 7th Grade Math Resources

7 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #161 : Plane Geometry

What is the area of a circle that has a diameter of inches?

Possible Answers:

706.8583

153.938

960

940

176.7146

153.938

940

Correct answer:

176.7146

Explanation:

The formula for finding the area of a circle is $\pi r^{2}$ . In this formula, represents the radius of the circle. Since the question only gives us the measurement of the diameter of the circle, we must calculate the radius. In order to do this, we divide the diameter by .

$\frac{15}{2}=7.5$

Now we use 7.5 for in our equation.

$\pi (7.5)^{2}=176.7146 \: in^{2}$

Report an Error

Example Question #231 : Ssat Upper Level Quantitative (Math)

What is the area of a circle with a diameter equal to 6?

Possible Answers:

$36\pi$

$3\pi$

$9\pi$

$18\pi$

Correct answer:

$9\pi$

Explanation:

First, solve for radius:

$r=\frac{d}{2}=\frac{6}{2}=3$

Then, solve for area:

$A=r^2\pi=3^2\pi=9\pi$

Report an Error

Example Question #4 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

The diameter of a circle is $4\ cm$ . Give the area of the circle.

Possible Answers:

$11.56\ cm^2$

$13\ cm^2$

$12.56\ cm^2$

$13.56\ cm^2$

$12 \ cm^2$

Correct answer:

$12.56\ cm^2$

Explanation:

The area of a circle can be calculated using the formula:

$Area=\frac{\pi d^2}{4}$ ,

where is the diameter of the circle, and $\pi$ is approximately 3.14 .

$Area=\frac{\pi d^2}{4}=\frac{\pi\times 4^2}{4}=4\pi \Rightarrow Area\approx 4\times 3.14\Rightarrow Area\approx 12.56 \ cm^2$

Report an Error

Example Question #232 : Ssat Upper Level Quantitative (Math)

The diameter of a circle is . Give the area of the circle in terms of .

Possible Answers:

11.56 t^2

11.56 t

12.56 t

12 t^2

12.56 t^2

Correct answer:

12.56 t^2

Explanation:

The area of a circle can be calculated using the formula:

$Area=\frac{\pi d^2}{4}$ ,

where is the diameter of the circle and $\pi$ is approximately 3.14 .

$Area=\frac{\pi (4t)^2}{4}=\frac{16\pi t^2}{4}=4\pi t^2 \Rightarrow Area\approx 4\times 3.14\times t^2$

$\Rightarrow Area\approx 12.56t^2$

Report an Error

Example Question #6 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

The radius of a circle is $\frac{2}{\sqrt{\pi }}$ . Give the area of the circle.

Possible Answers:

$4\pi$

$\frac{4}{\pi }$

$2\pi$

Correct answer:

Explanation:

The area of a circle can be calculated as $Area=\pi r^2$ , where is the radius of the circle, and $\pi$ is approximately 3.14 .

$Area=\pi r^2=\pi\times (\frac{2}{\sqrt{\pi}})^2=\pi\times \frac{4}{\pi}\Rightarrow Area=4$

Report an Error

Example Question #1 : Area Of A Circle

The circumference of a circle is 12.56 inches. Find the area of the circle.

Let $\pi = 3.14$ .

Possible Answers:

$11\ in^2$

$12\ in^2$

$11.56\ in^2$

$13.56\ in^2$

$12.56\ in^2$

Correct answer:

$12.56\ in^2$

Explanation:

First we need to find the radius of the circle. The circumference of a circle is $Circumference =2\pi r$ , where is the radius of the circle.

$12.56=2\times 3.14\times r\Rightarrow r=2\ in$

The area of a circle is $Area=\pi r^2$ where is the radius of the circle.

$Area=\pi r^2=3.14\times 2^2=12.56\ in^2$

Report an Error

Example Question #1 : Circles

The radius of a circle is 4 cm, what is the area?

Possible Answers:

$50.2\ cm^{2}$

$28.3\ cm^{2}$

$58.7\ cm^{2}$

$78\ cm^{2}$

$12.6\ cm^{2}$

Correct answer:

$50.2\ cm^{2}$

Explanation:

The area of a circle is found by: $Area=r^{2}\pi$ , where r is the radius.

$4^{2} \pi = 50.2$ .

The area of the circle is $50.2\ cm^{2}$ .

Report an Error

Example Question #1 : How To Find The Area Of A Circle

The radius, , of the circle below is 18 units. What is the area of the circle?

Circle

Possible Answers:

$18\pi$ square units

$36\pi$ square units

324 square units

$324\pi$ square units

Cannot be determined

Correct answer:

$324\pi$ square units

Explanation:

The formula for the area, , of a circle with radius is:

$A=\pi R^{2}$

We can fill in

$A=\pi (18^{2})$

$A=324\pi$

You could do the arithmetic to get an area of about 1,017.876 square units, but it is ok and more precise to leave it as shown.

Report an Error

Example Question #1 : Circles

Give the area of a circle with diameter 13.

Possible Answers:

$\frac{169\pi }{4}$

$\frac{169\pi }{2}$

$\frac{13\pi }{2}$

$26 \pi$

$13 \pi$

Correct answer:

$\frac{169\pi }{4}$

Explanation:

Half of the diameter 13 is the radius $\frac{13}{2}$ . Use the area formula:

$A = \pi r^{2} = \pi \cdot \left ( \frac{13}{2} \right )^{2} = \frac{169\pi }{4}$

Report an Error

Example Question #2 : Area Of A Circle

How many times greater is the area of a circle with a radius of 4in., compared to a circle with a radius of 2in.?

Possible Answers:

$4\pi$

$2\pi$

$4$

$\pi$

$2$

Correct answer:

$4$

Explanation:

The area of a circle can be solved using the equation $A=\pi r^{2}$

The area of a circle with radius 4 is $\pi 4^{2}=16\pi$ while the area of a circle with radius 2 is $\pi 2^{2}=4\pi$ . $16\pi \div 4\pi =4$

Report an Error

View Tutors

David
Certified Tutor

Kent State University, Bachelors, Marketing. Kent State University at Kent, Masters in Education, Special Education.

View Tutors

Alena
Certified Tutor

Mogilevsky State Pedagogical Institute, Bachelor in Arts, Mathematics. Mogilevsky State Pedagogical Institute, Masters, Mathe...

View Tutors

Rainier
Certified Tutor

Norfolk State University, Bachelors, Physics.

All Common Core: 7th Grade Math Resources

7 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Houston, Reading Tutors in Washington DC, Spanish Tutors in Philadelphia, ISEE Tutors in New York City, Algebra Tutors in Denver, GRE Tutors in Atlanta, GMAT Tutors in Dallas Fort Worth, Biology Tutors in Chicago, SSAT Tutors in Seattle, Biology Tutors in Philadelphia

Popular Courses & Classes

GMAT Courses & Classes in Los Angeles, GRE Courses & Classes in Chicago, ISEE Courses & Classes in Los Angeles, MCAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Miami, LSAT Courses & Classes in San Diego, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in Miami, GRE Courses & Classes in San Diego, Spanish Courses & Classes in Washington DC

Popular Test Prep

GRE Test Prep in Philadelphia, MCAT Test Prep in Houston, ACT Test Prep in Denver, GRE Test Prep in Phoenix, GRE Test Prep in San Diego, GMAT Test Prep in Seattle, GMAT Test Prep in Los Angeles, LSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Miami, SAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 7th Grade Math : Area of a circle

Study concepts, example questions & explanations for Common Core: 7th Grade Math

All Common Core: 7th Grade Math Resources

Example Questions

Example Question #161 : Plane Geometry

Example Question #231 : Ssat Upper Level Quantitative (Math)

Example Question #4 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

Example Question #232 : Ssat Upper Level Quantitative (Math)

Example Question #6 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

Example Question #1 : Area Of A Circle

Example Question #1 : Circles

Example Question #1 : How To Find The Area Of A Circle

Example Question #1 : Circles

Example Question #2 : Area Of A Circle

All Common Core: 7th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: