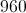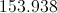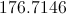We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 7th Grade Math : Know and Use the Formulas for the Area and Circumference of a Circle: CCSS.Math.Content.7.G.B.4

Study concepts, example questions & explanations for Common Core: 7th Grade Math

Create An Account

All Common Core: 7th Grade Math Resources

7 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find Circumference

The area of a circle is 25t^2 . Give the circumference of the circle in terms of .

Let $\pi=3.14$ .

Possible Answers:

20t

17.71 t^2

17.71t

20t^2

15t

Correct answer:

17.71t

Explanation:

The area of a circle can be calculated as $Area=\pi r^2$ , where is the radius of the circle.

$Area=\pi r^2\Rightarrow 25t^2=\pi r^2\Rightarrow r^2=\frac{25t^2}{\pi}$

$\Rightarrow r=\frac{5t}{\sqrt{\pi}}=\frac{5t}{\sqrt{3.14}}\approx 2.82t$

The circumference can be calculated as $Circumference =2\pi r$ , where is the radius of the circle.

$Circumference =2\pi r\Rightarrow Circumference =2\times 3.14\times 2.82t=17.71t$

Report an Error

Example Question #3 : Perimeter

The perimeter of a given rectangle is equal to the circumference of a given circle. The circle has radius inches; the width of the rectangle is $8 \pi$ inches. What is the length of the rectangle?

Possible Answers:

$7\pi$ inches

$14 \pi$ inches

$22 \pi$ inches

$44 \pi$ inches

$(30 - 8 \pi )$ inches

Correct answer:

$22 \pi$ inches

Explanation:

The circumference of a circle with radius inches is

$C = 2 \pi r = 2 \pi \cdot 30 = 60 \pi$ inches.

The perimeter of the rectangle is therefore $60 \pi$ inches. To find its length, substitute $W = 8\pi$ and $P = 60\pi$ into the equation and solve for :

2 L + 2W = P

$2 L + 2 \cdot 8 \pi = 60 \pi$

$2 L + 16 \pi = 60 \pi$

$2 L + 16 \pi - 16 \pi = 60 \pi - 16 \pi$

$2 L =44 \pi$

$2 L \div 2=44 \pi \div 2$

$L = 22\pi$ inches

Report an Error

Example Question #211 : Problem Solving

A manufacturer makes wooden circles out of square blocks of wood. If the wood costs $0.25 per square inch, what is the minimum waste cost possible for cutting a circle with a radius of 44 in.?

Possible Answers:

5808 dollars

1936π dollars

1936 dollars

7744 – 1936π dollars

1936 – 484π dollars

Correct answer:

1936 – 484π dollars

Explanation:

The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.) Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 88 inches for our problem. Its total area would be 88 * 88 or 7744 in².

Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr² or π * 44² = 1936π in². Therefore, the area remaining would be 7744 – 1936π. The cost of the waste would be 0.25 * (7744 – 1936π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 4 from our subtraction. This would give us: 0.25 * 4 * (1936 – 484π). Since 0.25 is equal to 1/4, 0.25 * 4 = 1. Therefore, our final answer is: 1936 – 484π dollars.

Report an Error

Example Question #1 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

A manufacturer makes wooden circles out of square blocks of wood. If the wood costs $0.20 per square inch, what is the minimum waste cost possible for cutting a circle with a radius of 25 in.?

Possible Answers:

625 - 25π dollars

625 dollars

500 dollars

2500 - 625π dollars

500 - 125π dollars

Correct answer:

500 - 125π dollars

Explanation:

The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.) Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 50 inches for our problem. Its total area would be 50 * 50 or 2500 in².

Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr² or π * 25² = 625π in². Therefore, the area remaining would be 2500 - 625π. The cost of the waste would be 0.2 * (2500 – 625π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 5 from our subtraction. This would give us: 0.2 * 5 * (500 – 125π). Since 0.2 is equal to 1/5, 0.2 * 625 = 125. Therefore, our final answer is: 500 – 125π dollars.

Report an Error

Example Question #1 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

What is the circumference of the circle provided?

Possible Answers:

$61\pi\textup{ in}$

$60\pi\textup{ in}$

$64\pi\textup{ in}$

$62\pi\textup{ in}$

$63\pi\textup{ in}$

Correct answer:

$64\pi\textup{ in}$

Explanation:

In order to solve this problem, we need to recall the formula for the circumference of a circle:

$C=2r\pi$ or $C=d\pi$

The circle in this question provides us with the radius, so we can use the first formula to solve:

$C=2(32)\pi$

Solve:

$C=64\pi\textup{ in}$

Report an Error

Example Question #1 : Area Of A Circle

What is the area of a circle that has a diameter of inches?

Possible Answers:

960

153.938

706.8583

153.938

176.7146

960

940

Correct answer:

176.7146

Explanation:

The formula for finding the area of a circle is $\pi r^{2}$ . In this formula, represents the radius of the circle. Since the question only gives us the measurement of the diameter of the circle, we must calculate the radius. In order to do this, we divide the diameter by .

$\frac{15}{2}=7.5$

Now we use 7.5 for in our equation.

$\pi (7.5)^{2}=176.7146 \: in^{2}$

Report an Error

Example Question #1 : Area Of A Circle

What is the area of a circle with a diameter equal to 6?

Possible Answers:

$3\pi$

$9\pi$

$18\pi$

$36\pi$

Correct answer:

$9\pi$

Explanation:

First, solve for radius:

$r=\frac{d}{2}=\frac{6}{2}=3$

Then, solve for area:

$A=r^2\pi=3^2\pi=9\pi$

Report an Error

Example Question #1 : Area Of A Circle

The diameter of a circle is $4\ cm$ . Give the area of the circle.

Possible Answers:

$12 \ cm^2$

$11.56\ cm^2$

$13\ cm^2$

$13.56\ cm^2$

$12.56\ cm^2$

Correct answer:

$12.56\ cm^2$

Explanation:

The area of a circle can be calculated using the formula:

$Area=\frac{\pi d^2}{4}$ ,

where is the diameter of the circle, and $\pi$ is approximately 3.14 .

$Area=\frac{\pi d^2}{4}=\frac{\pi\times 4^2}{4}=4\pi \Rightarrow Area\approx 4\times 3.14\Rightarrow Area\approx 12.56 \ cm^2$

Report an Error

Example Question #2 : Area Of A Circle

The diameter of a circle is . Give the area of the circle in terms of .

Possible Answers:

11.56 t^2

12.56 t

12.56 t^2

12 t^2

11.56 t

Correct answer:

12.56 t^2

Explanation:

The area of a circle can be calculated using the formula:

$Area=\frac{\pi d^2}{4}$ ,

where is the diameter of the circle and $\pi$ is approximately 3.14 .

$Area=\frac{\pi (4t)^2}{4}=\frac{16\pi t^2}{4}=4\pi t^2 \Rightarrow Area\approx 4\times 3.14\times t^2$

$\Rightarrow Area\approx 12.56t^2$

Report an Error

Example Question #3 : How To Find The Area Of A Circle

The radius of a circle is $\frac{2}{\sqrt{\pi }}$ . Give the area of the circle.

Possible Answers:

$4\pi$

$2\pi$

$\frac{4}{\pi }$

Correct answer:

Explanation:

The area of a circle can be calculated as $Area=\pi r^2$ , where is the radius of the circle, and $\pi$ is approximately 3.14 .

$Area=\pi r^2=\pi\times (\frac{2}{\sqrt{\pi}})^2=\pi\times \frac{4}{\pi}\Rightarrow Area=4$

Report an Error

View Tutors

Sarah
Certified Tutor

New York University, Bachelor of Fine Arts, Drama.

View Tutors

David
Certified Tutor

Kent State University, Bachelors, Marketing. Kent State University at Kent, Masters in Education, Special Education.

View Tutors

Rainier
Certified Tutor

Norfolk State University, Bachelors, Physics.

All Common Core: 7th Grade Math Resources

7 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Philadelphia, Algebra Tutors in Denver, Math Tutors in Phoenix, SSAT Tutors in Denver, Spanish Tutors in Atlanta, Reading Tutors in Boston, GRE Tutors in Phoenix, GMAT Tutors in Washington DC, Chemistry Tutors in New York City, ACT Tutors in Philadelphia

Popular Courses & Classes

LSAT Courses & Classes in San Diego, ACT Courses & Classes in Los Angeles, SSAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Philadelphia, SSAT Courses & Classes in New York City, LSAT Courses & Classes in Philadelphia, ACT Courses & Classes in Miami, MCAT Courses & Classes in Miami, Spanish Courses & Classes in Washington DC, SAT Courses & Classes in Washington DC

Popular Test Prep

SAT Test Prep in Washington DC, SSAT Test Prep in Boston, SSAT Test Prep in Denver, ACT Test Prep in Los Angeles, ACT Test Prep in Houston, SAT Test Prep in Houston, SAT Test Prep in Los Angeles, MCAT Test Prep in Miami, LSAT Test Prep in San Diego, LSAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 7th Grade Math : Know and Use the Formulas for the Area and Circumference of a Circle: CCSS.Math.Content.7.G.B.4

Study concepts, example questions & explanations for Common Core: 7th Grade Math

All Common Core: 7th Grade Math Resources

Example Questions

Example Question #2 : How To Find Circumference

Example Question #3 : Perimeter

Example Question #211 : Problem Solving

Example Question #1 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

Example Question #1 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

Example Question #1 : Area Of A Circle

Example Question #1 : Area Of A Circle

Example Question #1 : Area Of A Circle

Example Question #2 : Area Of A Circle

Example Question #3 : How To Find The Area Of A Circle

All Common Core: 7th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: